【応用情報技術者】OC曲線とは何か
●OC曲線とは
ロットの抜き取り検査を行った時の、ロットの合格率と製品の不良率の関係性を表したグラフ
●出題された回(平成29年度春期以降)
平成30年度秋期/平成30年度春期
OC曲線の説明
OC曲線とは、検査特性曲線とも呼ばれ、ロットの抜き取り検査を行った時の、ロットの合格率と製品の不良率の関係性を表したグラフです。
ロットとは
ロットとは、製品を管理するグループのことです。
例えば、2023年5月6日に工場Aで製造された椅子をロット番号「20230506A」、2023年5月7日に工場Bで製造された椅子をロット番号「20230507B」として管理します。
なぜ、このような管理をするのでしょうか?
例えば、お客さんから購入した椅子が壊れているとクレームが入り、調査してみると製造の過程で重要なミスがあり、2023年5月6日に工場Aで作られた椅子は回収しないといけないと分かったとしましょう。
この時、ロット番号を割り振っていれば、ロット番号「20230506A」の製品を回収すれば良いとすぐに分かります。ロット番号を使うことで、製品の管理がしやすくなるという訳です。
ロットの抜取検査とは
どんな製品でも出荷する前に、不良品を取り除かなければいけません。でも、製造した製品を全て検査していくのはコストが掛かります。
そこで、製造した製品の中から一部を抜き出して検査をします。これを抜取検査と言います。
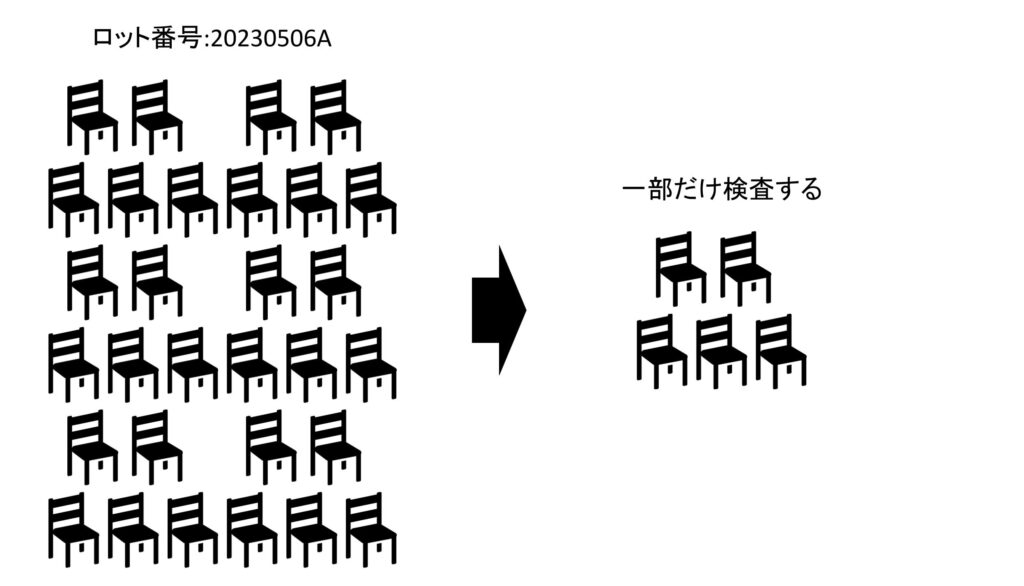
例えば、ロット番号「20230506A」の椅子から5脚を抜き出して検査した時、4脚合格ならロット番号「20230506A」の椅子を合格とし、2脚以上不良品が含まれればロット番号「20230506A」を不合格とする。のような検査をします。これが抜取検査です。
抜取検査はコストを抑えることが出来ますが、その分リスクもあります。
抜取検査のリスク

100脚の椅子から5脚を抜き出して不良品が1脚以下ならロットを合格とするような検査を考えます。
例えば、100脚中2脚しか不良品ないのに、たまたま抜き出した5脚の中に不良品の2脚が存在すれば、そのロットは不合格となってしまいます。
また、100脚中90脚も不良品があるのに、たまたま抜き出した5脚全部が合格ならば、そのロットは合格となってしまいます。
このように、抜取検査には本来合格にすべきロットが不合格になったり、不合格にすべきロットが合格になるリスクが存在するのです。
そこで、抜取検査にどの程度リスクがあるのかを見極めるのに使われるのがOC曲線です。
OC曲線とは
OC曲線とは、ロットの抜き取り検査を行った時の、ロットの合格率と製品の不良率の関係性を表したグラフです。
例えば、下のグラフはロットから100個のサンプルを抜き出して不良品が1個以下の場合は合格とする時のOC曲線です。
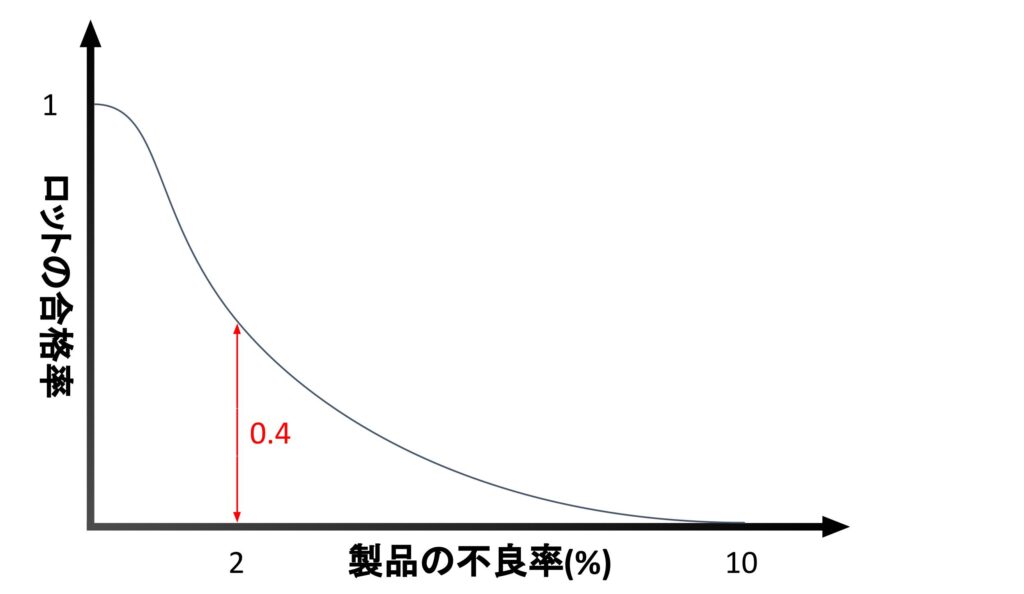
実際の製品の不良率が2%だった場合、ロットの合格率は0.4、つまり、40%のロットが合格になることが分かります。このようにロットの合格率と製品の不良率の関係性を表したのがOC曲線です。
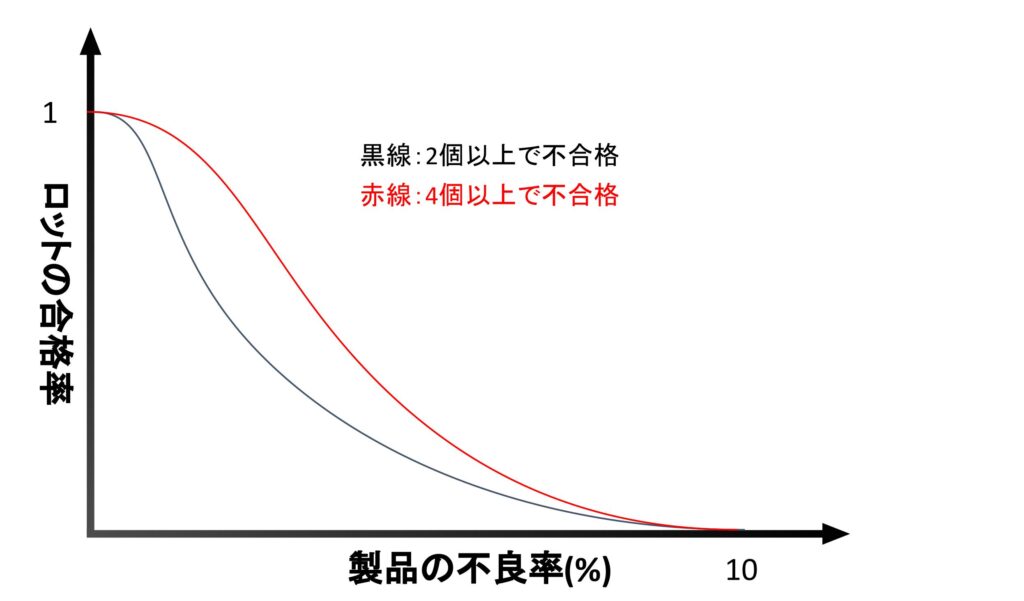
OC曲線はロットから抜き出すサンプルの数と合格基準となる不良品の数によって変化します。
100個のサンプルの内2個以上不良品があれば不合格としていたのを、4個以上不良品があれば不合格とすれば、その分、ロットの合格率は上がりますよね。
不良率が低いのにロットの合格率が低いと、その分、生産者が損しますが、逆に、
不良率が高いのにロットの合格率が高いと、その分、消費者が損します。
良い感じの所を見つけるためにOC曲線が使われているという訳です。
過去問
応用情報技術者 午前試験
平成30年度秋期問75
横軸にロットの不良率,縦軸にロットの合格率をとり,抜取検査でのロットの品質とその合格率の関係を表したものはどれか。
ア OC曲線
イ バスタブ曲線
ウ ポアソン分布
エ ワイブル分布
正解は”ア”
応用情報技術者 午前試験
平成30年度春期問74
図は,ある製品ロットの抜取り検査の結果を表すOC曲線(検査特性曲線)である。この図が表しているものはどれか。
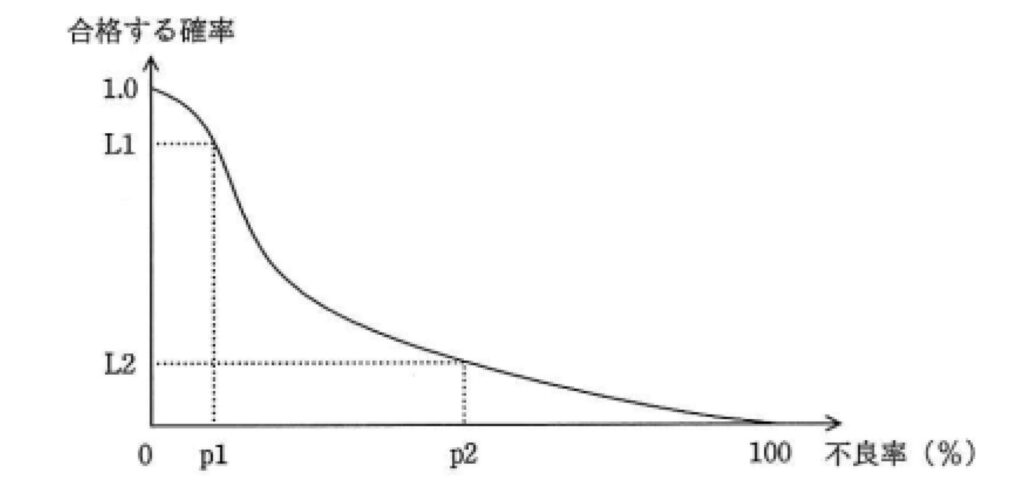
ア p1%よりも大きい不良率のロットが合格する確率は,L1よりも大きい。
イ p1%よりも小さい不良率のロットが不合格となる確率は,(1.0-L1)よりも大きい。
ウ p2%よりも大きい不良率のロットが合格する確率は,L2よりも小さい。
エ p2%よりも小さい不良率のロットが不合格となる確率は,L2よりも小さい。
正解は”ウ”
ア 不良率が大きければ、その分、合格になる確率も小さくなるはずです。よって誤りとなります。
イ 不良率が小さければ、その分、不合格になる確率も小さくなるはずです。よって誤りとなります。
ウ 不良率が大きければ、その分、合格になる確率も小さくなるはずです。よって正しいです。
エ 不良率が小さければ、その分、不合格になる確率も小さくなるはずです。よって誤りとなります。


