【基本情報】初心者向け!関数の解き方を分かりやすく解説!
この記事では、関数の問題の解き方について、初心者にも分かりやすく、図解付きで丁寧に解説しています!
関数
- 関数とは受け取った数字や文字列に対して、結果を返すプログラムの部品。
- 関数が受け取る値を引数、処理結果を戻り値と呼ぶ。
- 関数は「f(n)=nを含む計算式」と表記する。nが引数、計算結果が戻り値。
- 再帰的な関数は、計算式の中に自分自身の関数を含む関数。
関数とは
関数とは受け取った数字とか文字列に対して、結果を返すプログラムの部品です。関数が受け取る値を引数、処理の結果を戻り値と呼びます。
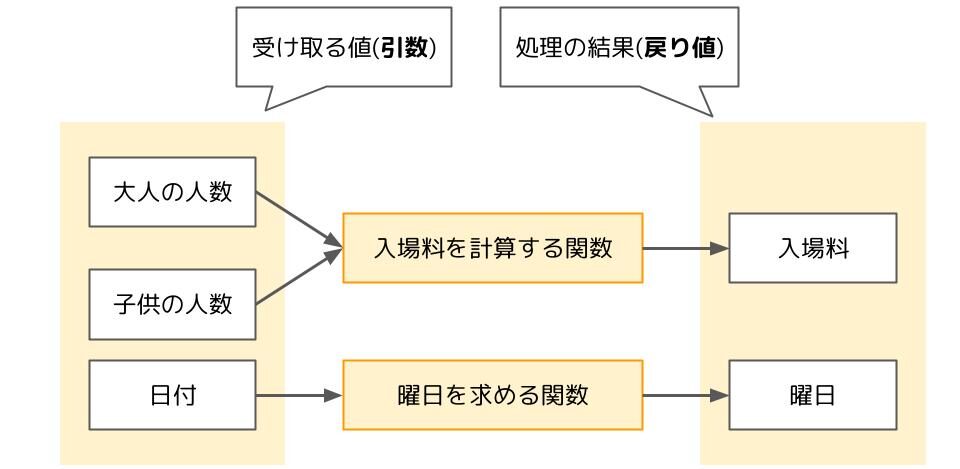
関数の中には戻り値が無いものもあります。例えば、ログインを押したら「ようこそ!」と表示する関数には戻り値がありません。全く覚える必要はありませんが、基本情報では戻り値がない関数を「手続き」と呼びます。
関数の書き方
関数は「f(n)=nを含んだ計算式」と表記します。nが引数で計算結果が戻り値ですね。引数が複数ある場合は「f(n,m)=nとmを含んだ計算式」と表記します。

また、引数によって計算式が変わる場合は「f(n):nの条件 then return 条件を満たす時の戻り値 else 条件を満たさない時の戻り値」と表記します。入場者の数が4人以上なら割引される入園料を計算する関数はこんな感じですね。

この場合、入場者が3人なら1000×3=3000、入場者が4人なら800×4=3200となります。
再帰的な関数
関数の中に自分自身を呼び出すことが出来る処理が含まれるような関数を再帰的な関数と呼びます。
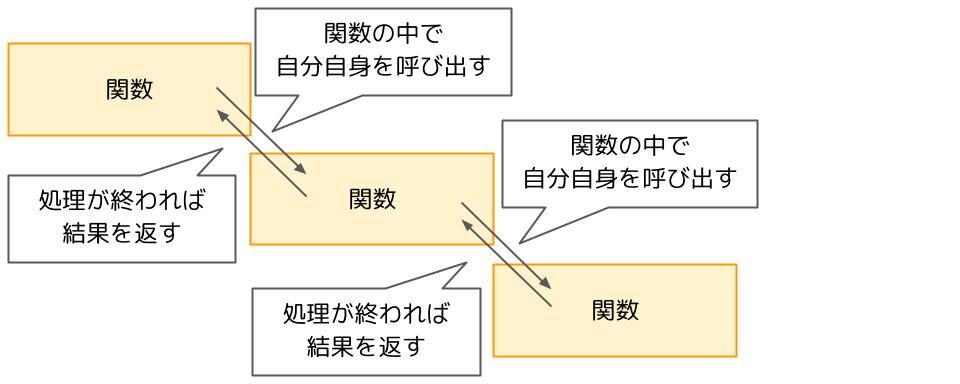
再帰的の例を見てみましょう。「1からnまでの整数を足し算した結果を返す関数」はこのようになります。
f(n):if n=1 then return 1 else return n+f(n-1)
・n=1の時、戻り値=1
・n=1以外の時、戻り値=n+f(n-1)
n=1以外の時の戻り値には、f(n-1)と自分自身が含まれていますね。これが再帰的です。では、実際に計算してみましょう。n=1~5の時の結果はそれぞれこのようになります。
・n=5のときf(5)=5+f(4)
・n=4のときf(4)=4+f(3)
・n=3のときf(3)=3+f(2)
・n=2のときf(2)=2+f(1)
・n=1のときf(1)=1
f(5)=5+f(4)なので、
f(5)=5+(4+f(3))=9+f(3)=9+(3+f(2))=12+f(2)=12+(2+f(1))=14+f(1)
=14+1=15となります。
このように、処理の中で自分自身を呼び出すような関数を再帰的な関数と言います。
基本情報技術者試験での出題例
サンプル問題問8、令和元年度秋期問11
基本情報技術者
科目A サンプル問題問8、午前試験 令和元年度秋期問11
自然数nに対して,次のとおり再帰的に定義される関数f(n)を考える。f(5)の値はどれか。
f(n):if n≦1 then return 1 else return n+f(n-1)
ア 6 イ 9 ウ 15 エ 25
正解は”ウ”
関数f(n)の戻り値は
・引数が1の場合、1
・引数が1以外の場合、n+f(n-1)
f(5)
=5+f(4) 【引数が5なので、f(5)=5+f(4)】
=5+(4+f(3)) 【引数が4なので、f(4)=4+f(3)】
=9+f(3)
=9+(3+f(2)) 【引数が3なので、f(3)=3+f(2)】
=12+f(2)
=12+(2+f(1)) 【引数が2なので、f(2)=2+f(1)】
=12+2+1 【引数が1なので、f(1)=1】
=15
よって、答えは15です。
令和元年度秋期問4
基本情報技術者
午前試験 令和元年度秋期問4
a及びbを定数とする関数 f(t)=\(\displaystyle \frac{a}{t+1}\)及び g(t)=\(\displaystyle \frac{b}{t²-1}\)に対して,\(\displaystyle \lim_{t \to \infty}\frac{g(t)}{f(t)}\)はどれか。ここで,a≠0,b≠0,t>1とする。
ア 0 イ 1 ウ \(\frac{b}{a}\) エ \(\infty\)
正解は”ア”
まず、\(\displaystyle \lim_{t \to \infty}\frac{g(t)}{f(t)}\)の記号の意味について解説しておきます。\(\displaystyle \lim_{t \to \infty}f(t)\)は関数f(t)の引数であるtを無限大にした時の戻り値を意味します。
例えば、f(t)=t+2の場合、tを無限大にすればf(t)も無限大になるので、\(\displaystyle \lim_{t \to \infty}f(t)\)=\(\infty\)となります。
f(t)=\(\displaystyle \frac{1}{t+2}\)の場合、tを無限大にすればf(t)は0になります。t=8の場合はf(t)=\(\displaystyle \frac{1}{10}\)=0.1で、t=9998の場合はf(t)=\(\displaystyle \frac{1}{10000}\)=0.0001でになります。tを大きくすれば大きくする程、f(t)は小さくなっているので、tを無限大にすればf(t)は0になりそうですよね。
tを無限大にすると言われても想像しにくいと思うので、t=10、100、1000と大きくしたときに戻り値がどうなるかを考えれば良いと思います。
では、問題を実際に解いていきましょう。
\(\displaystyle \frac{g(t)}{f(t)}\)
=\(\displaystyle \frac{b}{t²-t}\)×\(\displaystyle \frac{t+1}{a}\)
=\(\displaystyle \frac{b(t+1)}{a(t²-t)}\)・・・①
a、b、tに具体的に数字を入れてみましょう。
aとbは0以外ならなんでも良いので、両方1だとして考えてみます。
t=10を①に代入してみましょう。
①=\(\displaystyle \frac{11}{90}\)=約0.12
次にt=100を①に代入してみましょう。
①=\(\displaystyle \frac{101}{9900}\)=約0.0102
次にt=10000を①に代入してみましょう。
①=\(\displaystyle \frac{10001}{99990000}\)=約0.0001
tを大きくすれば戻り値は小さくなっていますね。このことから、tを無限大にすれば最終的に戻り値が0になるだろうと想像できます。よって答えはアです。
令和元年度秋期問6
基本情報技術者
午前試験 令和元年度秋期問6
Random(n)は,0以上n未満の整数を一様な確率で返す関数である。整数型の変数A,B及びCに対して次の一連の手続を実行したとき,Cの値が0になる確率はどれか。
A=Random(10)
B=Random(10)
C=A-B
ア \(\frac{1}{100}\) イ \(\frac{1}{20}\) ウ \(\frac{1}{10}\) エ \(\frac{1}{5}\)
正解は”ウ”
Random(10)は0以上10未満の整数を返すので、0,1,2,3,4,5,6,7,8,9を返します。
AとBの組み合わせは、
A=0のとき、B=0~9の10通り、
A=1のとき、B=0~9の10通り、
・
・
・
A=9のとき、B=0~9の10通り、で100通りあります。
このうち、C=0になるパターンは、
A=0のとき、B=0の1通り、
A=1のとき、B=1の1通り、
・
・
・
A=9のとき、B=9の1通り、で10通りあります。
よって、Cの値が0になる確率は\(\frac{10}{100}\)=\(\frac{1}{10}\)となります。
平成29年度春期問6
基本情報技術者
午前試験 平成29年度春期問6
関数 f(x,y)が次のように定義されているとき,f(775,527)の値は幾らか。ここで,x mod yはxをyで割った余りを返す。
f(x,y): if y = 0 then return x else return f(y,x mod y)
ア 0 イ 31 ウ 248 エ 527
正解は”イ”
関数f(x,y)の戻り値は
・引数yが0の場合、x
・引数yが0以外の場合、f(y, x mod y)
f(775,527)
=f(527, 775 mod 527) 【引数yが0ではないので】
=f(527, 248) 【775÷527=1余り248】
=f(248, 527 mod 248) 【引数yが0ではないので】
=f(248, 31) 【527÷248=2余り31】
=f(31, 248 mod 31) 【引数yが0ではないので】
=f(31, 0) 【248÷31=8余り0】
=31 【引数yが0なので戻り値はx】
よって、答えは31です。



