【応用情報】データの誤り制御:パリティチェックとハミング符号とCRCについて解説
この記事では、データの誤り制御方法であるパリティチェックとハミング符号とCRCについて、初心者にも分かりやすく、図解付きで丁寧に解説しています!
データの誤り
- データは電気信号で伝送される
- 伝送の途中で電気信号にノイズが入るとデータのビット内容が変わってしまうことがあり、それをデータの誤りと呼ぶ
パリティチェック
- パリティチェックではデータのビット列に対してパリティビットと呼ばれる誤り検知用のビットを与えることでデータの誤りを検知する
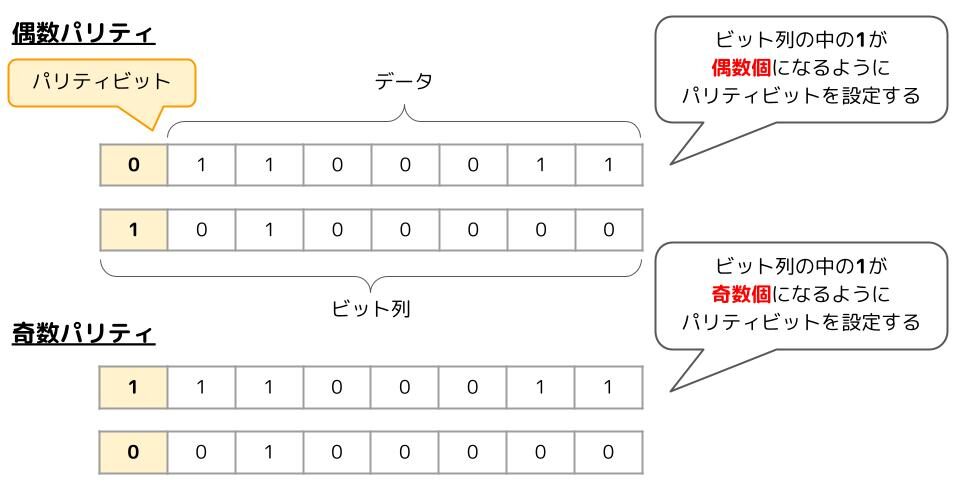
- 偶数パリティでは送信データ内の1が偶数個になるようにパリティビットを設定する
- 奇数パリティでは送信データ内の1が奇数個になるようにパリティビットを設定する
- 水平垂直パリティチェックでは縦と横からパリティチェックを行う
- 水平垂直パリティチェックでは1ビットの誤りを修正できる
ハミング符号
- ハミング符号ではデータのビット列に対して検査用の冗長ビットを与えることで誤りを検知する
- ハミング符号は2ビットまでの誤り検出と1ビットの誤り訂正が可能
CRC
- 送信データを特定の数字(生成多項式)で割り、その余りを検査用データとして、送信データに付加する方式
ビット誤り率
- ビット誤り率 = 誤りが発生したビット数 ÷ 送信ビット数
データの誤りとは
データの誤りとは、ビットの内容が0→1や1→0に意図せず変わってしまうことです。データは0と1のビットの集まりで表現されますが、実体はただの電気信号です。なので、伝送中に他の電気信号から干渉があれば電気信号が乱れることもありますし、長距離移動すれば電気信号が衰退することもあります。そんな理由から途中でデータの内容が微妙に変わってしまうことがあります。

そこでデータの誤りを検知したり、修正するためにパリティチェックやハミング符号という技術が使われます。
パリティチェック
パリティチェックでは、データのビット列に対してパリティビットと呼ばれる誤り検知用のビットを与えることでデータの誤りを検知します。
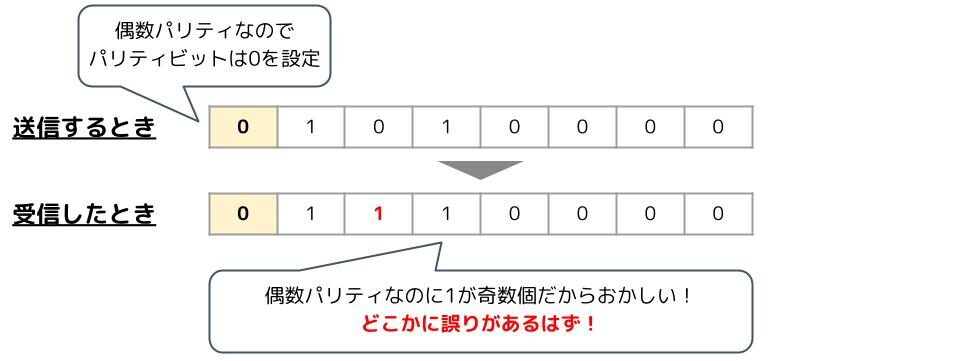
例えば偶数パリティで「1010000」というデータを送るとします。その時のパリティビットは0になりますね。しかし、データを受信した時に、データの一部が化けており「1110000」となっていれば、パリティビットと整合性が取れずにどこかがおかしいことが分かります。
しかし、偶数/奇数パリティで出来るのは「どこか1ビットが誤っていること」を検知するだけです。どこが誤っているかということは分からないので、誤りの訂正も出来ません。
水平垂直パリティチェック
水平垂直パリティチェックでは、縦と横からパリティチェックを行います。
例えば、「Hello」とデータを送る時、偶数パリティを使うとパリティビットはこうなります。
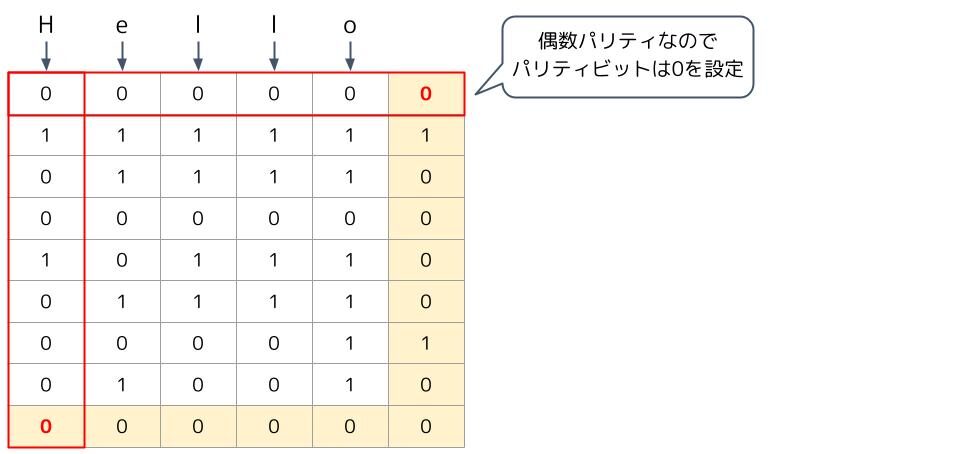
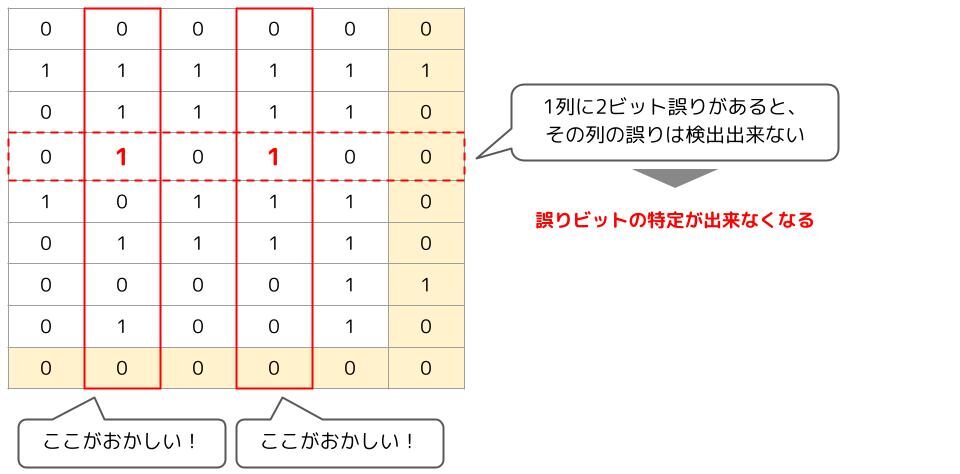
水平垂直パリティチェックでは、1ビットの誤りなら特定して訂正することが出来ます。
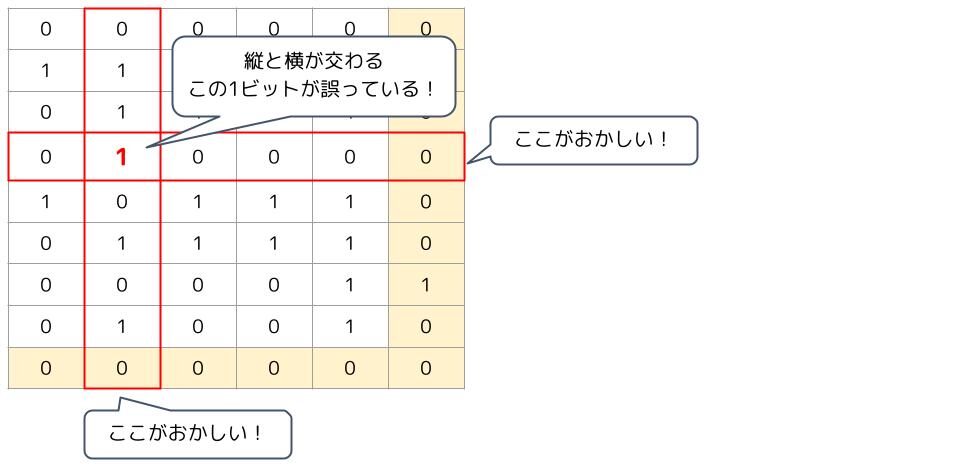
2ビット以上誤りがある場合は、誤りの位置を特定することは出来ません。
ハミング符号
ハミング符号は、データのビット列に対して検査用の冗長ビットを与えることで誤りを検知する技術です。
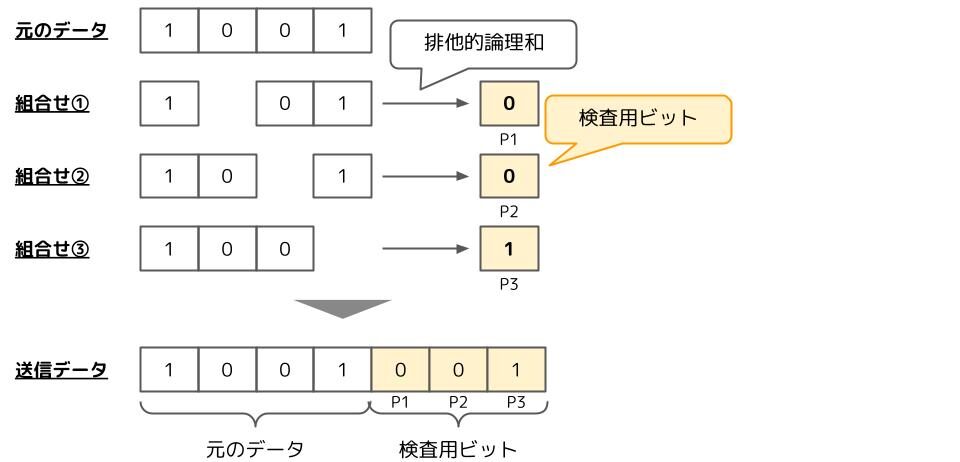
4ビットのデータに3ビットの検査用ビットを付与する場合を考えます。元のデータからビットを抜き取るパターンを3つ作り、1の数が偶数個になるように検査用ビットを設定します。少し難しい表現をすると、それぞれの組合せの排他的論理和が検査用ビットとなります。そして、元のデータに検査用ビットをくっつけたものを送信データとします。
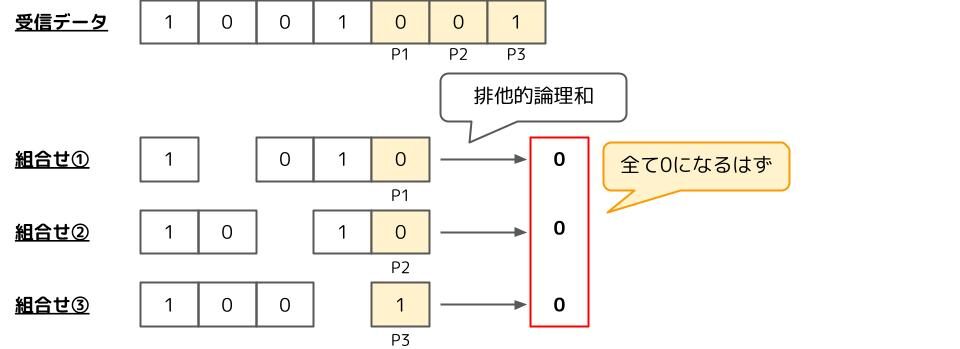
受信者は受信データから組合せ①~③を作り、それぞれの検査用ビットと合わせて1の数が偶数個かどうか検証します。難しい表現をすると、それぞれの排他的論理和が0になるはずです。
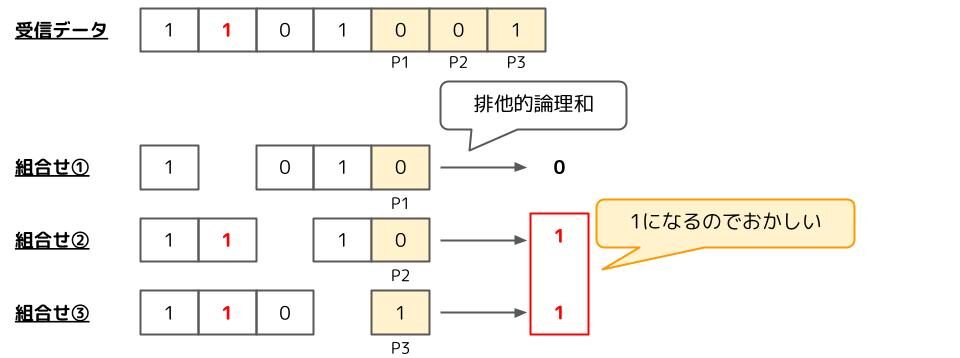
仮に伝送の途中でデータのビット列がおかしくなっていたらどうなるでしょうか。
排他的論理和を取った時に1になる組合せが出てきます。よって、データに誤りがあると判断出来るわけです。
2ビットまでの誤り検出と1ビットの誤り訂正が可能
ハミング符号は2ビットまでの誤り検出と1ビットの誤り訂正が可能であると言われます。
検証してみましょう。
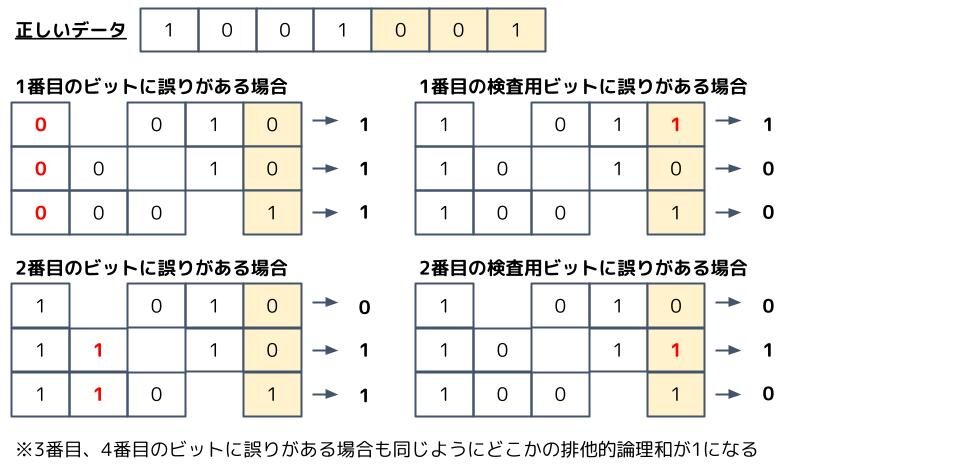
もし、送信データのうち1ビット誤りがある場合、このようになります。
全てのパターンで排他的論理和のどれかが1になっていますね。よって、1ビットの誤りは検知可能です。
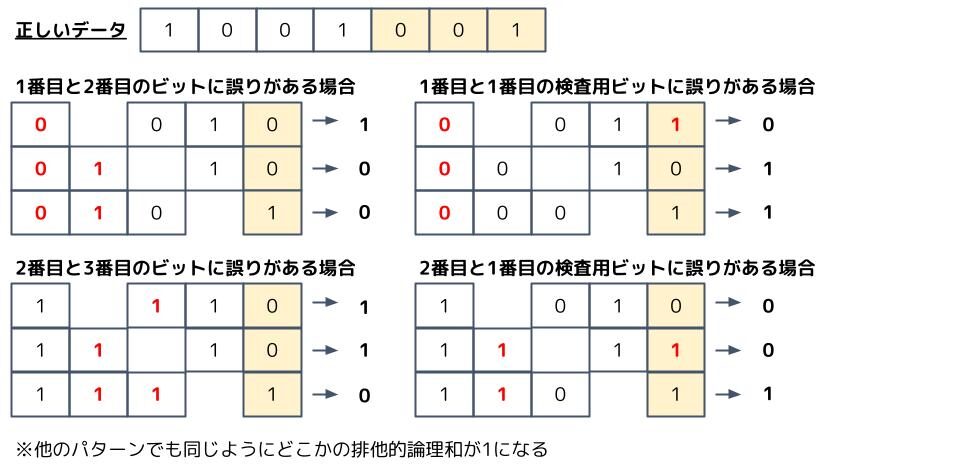
次に送信データのうち2ビット誤りがある場合、このようになります。
これも全てのパターンで排他的論理和のどれかが1になり、誤りを検知できることが分かります。
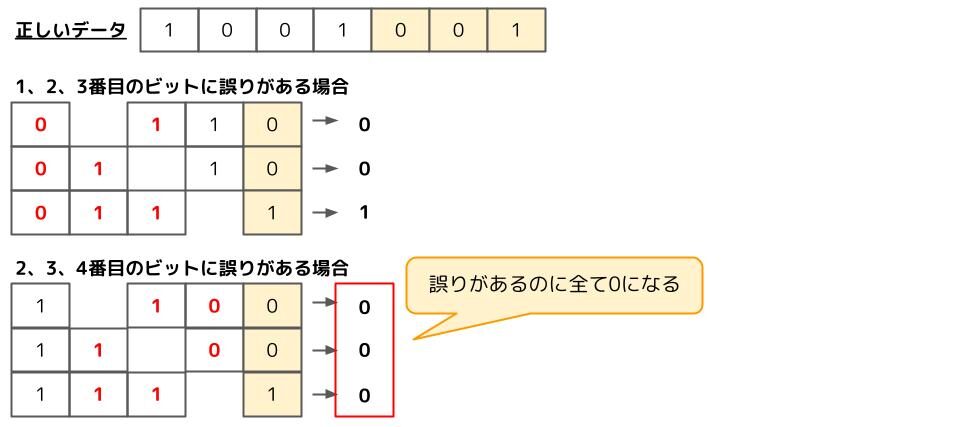
では、送信データのうち3ビット誤りがある場合、どうなるでしょうか。
誤りがあるのに、排他的論理和が全て0になることがあります。これでは誤りは検知出来ませんよね。よって、ハミング符号では2ビットまでの誤りは検知出来るが、3ビットの誤りは検知出来ないということが分かります。
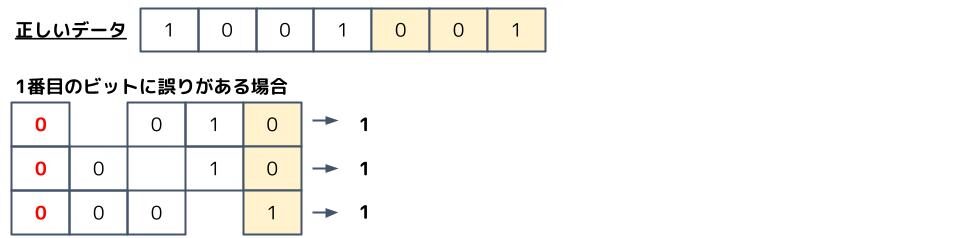
また、誤りが1ビットしか無い場合、全ての排他的論理和が1になっている時は1番目のビットに誤りがあると特定出来ます。なので、誤りが1ビットしか無い場合のみ誤りの訂正が可能になります。
CRC(巡回冗長検査)
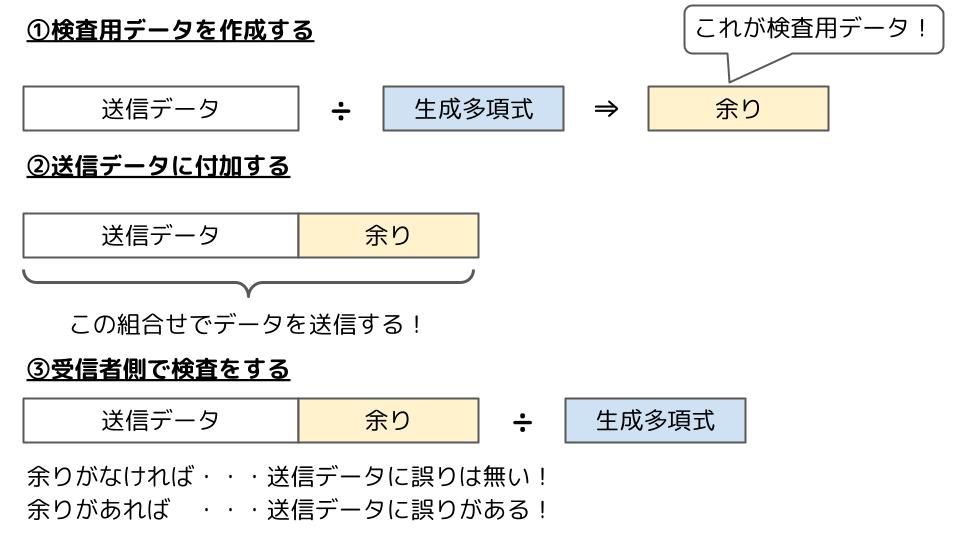
CRC(Cyclic Redundancy Check)は、送信データを特定の数字(生成多項式と言います)で割り、その余りを検査用データとして、送信データに付加する方式です。
送信者側で送信データと生成多項式から検査用データを作り、検査用データを送信データに付加して送ります。受信者側は送られたデータを生成多項式で割り、余りが出なければ誤りが無い!と判断します。
ビット誤り率
ビット誤り率とは、送信したビット数のうち、どれだけ誤りが生じたのかを表す値です。
ビット誤り率 = 誤りが発生したビット数 ÷ 送信ビット数
応用情報技術者試験での出題例
令和7年度秋期問4
応用情報技術者
午前試験 令和7年度秋期問4
誤り検出方式であるCRCに関する記述として,適切なものはどれか。
ア 検査用のデータは,検査対象のデータを生成多項式で処理して得られる1ビットの値である。
イ 受信側では,付加されてきた検査用のデータで検査対象のデータを割り,余りがなければ送信が正しかったと判断する。
ウ 送信側では,生成多項式を用いて検査対象のデータから検査用のデータを作り,これを検査対象のデータに付けて送信する。
エ 送信側と受信側では,異なる生成多項式が用いられる。
正解は”ウ”
CRCでは、送信者側で生成多項式を用いて検査用データを作り、送信データに付加します。受信者側は送信されてきたデータを生成多項式で割り、余りが出なければ誤り無しと判断します。よって、答えはウです。
令和7年度秋期問35
応用情報技術者
午前試験 令和7年度秋期問35
ビット誤り率が0.0001%の回線を使って,1,500バイトのパケットを10,000個送信するとき,誤りが含まれるパケットの個数の期待値はおよそ幾らか。
ア 10 イ 15 ウ 80 エ 120
正解は”エ”
1,500バイトは1,500×8=12,000ビットです。
よって、誤りが含まれるパケットは、12,000ビット×10,000個÷0.0001÷100=120個となります。
令和6年度春期問4
応用情報技術者
午前試験 令和6年度春期問4
符号長7ビット,情報ビット数4ビットのハミング符号による誤り訂正の方法を,次のとおりとする。
受信した7ビットの符号語x₁ x₂ x₃ x₄ x₅ x₆ x₇(xk=0又は1)に対して
c₀=x₁ +x₃ +x₅ +x₇
c₁= x₂+x₃ +x₆+x₇
c₂= x₄+x₅+x₆+x₇
(いずれもmod2での計算)
を計算し,c₀,c₁,c₂の中に少なくとも一つは0でないものがある場合には,
i=c₀+c₁×2+c₂×4
を求めて,左からiビット目を反転することによって誤りを訂正する。
受信した符号語が1000101であった場合,誤り訂正後の符号語はどれか。
ア 1000001 イ 1000101 ウ 1001101 エ 1010101
正解は”エ”
受信した符号語1000101からc₀,c₁,c₂を計算してみます。
c₀=(1+0+1+1)mod2=3mod2=1
c₁=(0+0+0+1)mod2=1mod2=1
c₂=(0+1+0+1)mod2=2mod2=0
0でないものがあるので、問題文の通りiを求めてみましょう。
i=1+1×2+0×4=3
よって、左から3番目を反転すれば誤りを訂正できることが分かります。
なので、誤り訂正後の符号語は1010101で答えはエとなります。
令和6年度春期問33
応用情報技術者
午前試験 令和6年度春期問33
ビット誤り率が0.0001%の回線を使って,1,500バイトのパケットを10,000個送信するとき,誤りが含まれるパケットの個数の期待値はおよそ幾らか。
ア 10 イ 15 ウ 80 エ 120
正解は”エ”
ビット誤り率は、次の式で表されます。
ビット誤り率 = 誤りが発生したビット数 ÷ 送信ビット数
よって、
1,500バイト×8×10,000個×0.0001%÷100=120
となるので、よって答えはエです。
令和5年度秋期問4、令和3年度秋期問4
応用情報技術者
午前試験 令和5年度秋期問4 令和3年度秋期問4
図のように16ビットのデータを4×4の正方形状に並べ,行と列にパリティビットを付加することによって何ビットまでの誤りを訂正できるか。ここで,図の網掛け部分はパリティビットを表す。
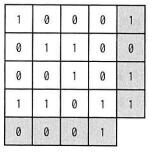
ア 1 イ 2 ウ 3 エ 4
正解は”ア”
水平垂直パリティチェックでは1ビットまでの誤りを訂正出来ます。よって答えはアです。
令和4年度春期問4
応用情報技術者
午前試験 令和4年度春期問4
ハミング符号とは,データに冗長ビットを付加して,1ビットの誤りを訂正できるようにしたものである。ここでは,X₁,X₂,X₃,X₄の4ビットから成るデータに,3ビットの冗長ビットP₃,P₂,P₁を付加したハミング符号X₁X₂X₃P₃X₄P₂P₁を考える。付加したビットP₁,P₂,P₃は,それぞれ
X₁⊕X₃⊕X₄⊕P₁=0
X₁⊕X₂⊕X₄⊕P₂=0
X₁⊕X₂⊕X₃⊕P₃=0
となるように決める。ここで,⊕は排他的論理和を表す。
ハミング符号1110011には1ビットの誤りが存在する。誤りビットを訂正したハミング符号はどれか。
ア 0110011 イ 1010011 ウ 1100011 エ 1110111
正解は”ア”
受信したハミング符号は1110011で、X₁X₂X₃P₃X₄P₂P₁なので、
X₁⊕X₃⊕X₄⊕P₁=1⊕1⊕0⊕1=1
X₁⊕X₂⊕X₄⊕P₂=1⊕1⊕0⊕1=1
X₁⊕X₂⊕X₃⊕P₃=1⊕1⊕0⊕0=1
となります。全ての排他的論理和が1で、全ての組合せに存在するビットはX₁だけなので、誤りビットはX₁だと分かります。
よってX₁のビットを1→0に修正した0110011が答えだと分かります。



