【応用情報】データの探索:線形探索法、2分探索法、ハッシュ法について解説
この記事では、データの探索方法である線形探索法、2分探索法、ハッシュ法について、初心者にも分かりやすく、図解付きで丁寧に解説しています!配列など複数の箱から特定のデータを探すことをデータの探索と言います。
線形探索法
- 線形探索法とは配列の前から探したいデータが見つかるまで探索し続ける方法
2分探索法
- 2分探索法は以下の方法でデータを探す方法
①データを昇順(小さいもの順)に並べる
②真ん中にある数字を見る
③②の数字と探したい数字を比較する
④探したい数字の方が小さい場合は前半の数字で②と③を行い、大きい場合は後半の数字で②と③を行う
⑤数字が見つかるまで②~④を繰り返す - 2分探索木は2分探索を図で表したもの
ハッシュ法
- ハッシュ法ではデータの格納場所をハッシュ関数に従って決定して、そこに格納する
線形探索法
線形探索法とは、配列の最初から目的のデータを見つけるまで探索する方法です。
データが存在しない場合は、最後まで探索して、見つからずに終了します。

2分探索法
2分探索法では、昇順に並んだ値からある値を探す時に、まず、中央の値と探したい値を比較し、探したい値が前半にあるか後半にあるかを明らかにする。そして検索範囲を絞り込んだら、再度、その範囲の中央の値と探したい値を比較し、探したい値がその範囲の前半にあるか後半にあるかを明らかにする。。。というのを繰り返しながら値を探します。2分探索法は小さい順、大きい順に並んでいる配列にしか使えません。
具体的に見てみましょう。
以下10個の箱にはランダムに10個の数字が格納されています。ただし、①から⑩に行くにつれて格納されている数字は大きくなります。ここから2分探索法で「25」を探してみましょう。まず中央の箱(⑤)を開けます。⑤には68が入っていたので、25は前半(①~④)にあることが分かります。

ということで次は①~④の中央の箱、③の箱を開けます(②でもOKです)。③には19が入っていたので、①~④の後半(④)にあることが分かります。

ということで④の箱を開けてみましょう。④には25が入っていました。

このように、
- 中央の値と探したい値を比較して、前半にあるか後半にあるかを明らかにする
- 絞った探索範囲の中央の値と探したい値を比較して、絞った探索範囲の中から更に前半にあるか後半にあるかを明らかにする
- 絞った探索範囲の中央の値と探したい値を比較して、絞った探索範囲の中から更に前半にあるか後半にあるかを明らかにする
- ・・・
- ・・・
というのを探したい値が見つかるまで繰り返すのが2分探索です。そして、2分探索法を分かりやすく図にしたものが2分探索木です。
2分探索木
2分探索木とは、2分探索できるデータの格納方法や2分探索ってどうやるの?という方法を分かりやすく図にしたものです。
先程の箱を全て開けてみましょう。

これらの数字を2分探索木に表すと下図のようになります。〇の部分を節(ノード)と言い、節と節を繋いだ線を枝(ブランチ)を言います。
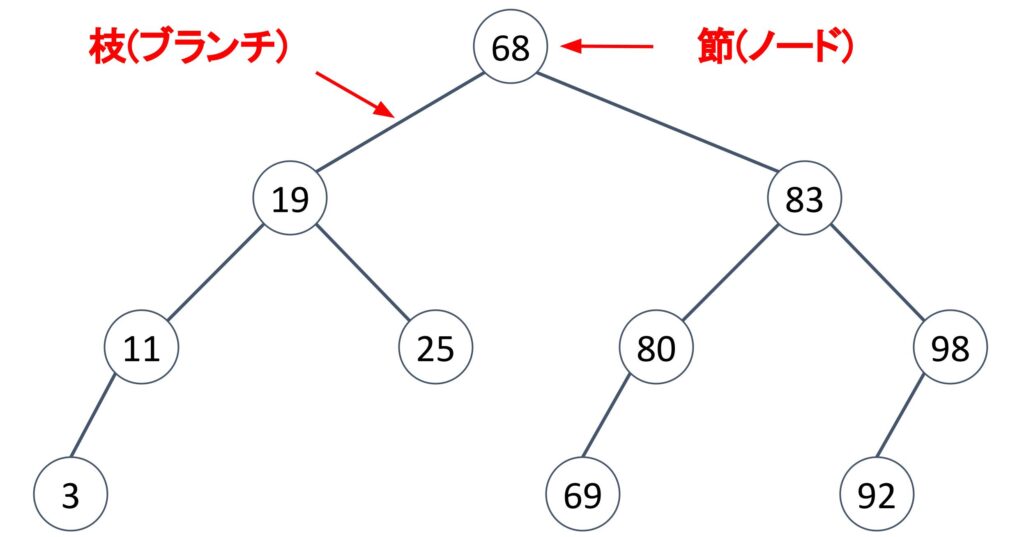
2分探索木には上の節より大きい数字は右側の節に、小さい数字は左側の節に格納するというルールがあります。
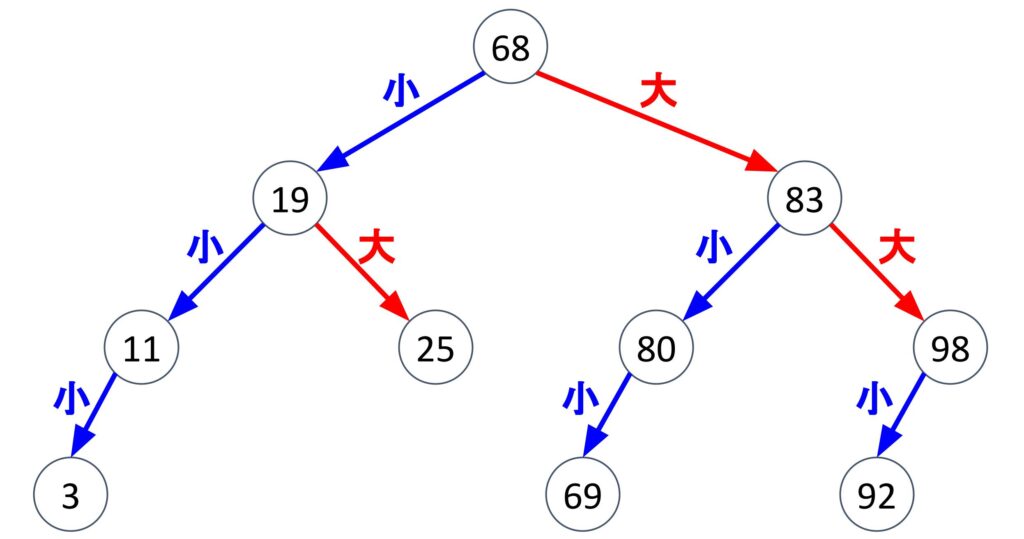
2分探索木を色々な視点で見てみる
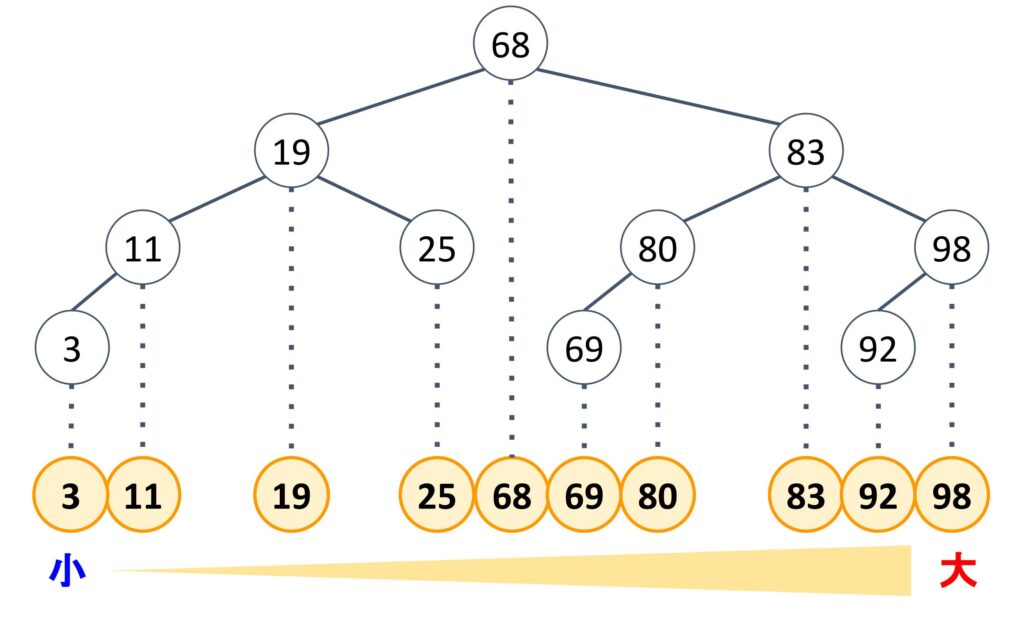
節の値を一番下に降ろして見ると……
節の値を一番下に降ろしてみましょう。すると、一番左が小さく、右に行くにつれて大きくなっていることが分かります。2分探索は値が昇順・降順になっていなければ出来ません。その特徴を表していることが分かりますね。
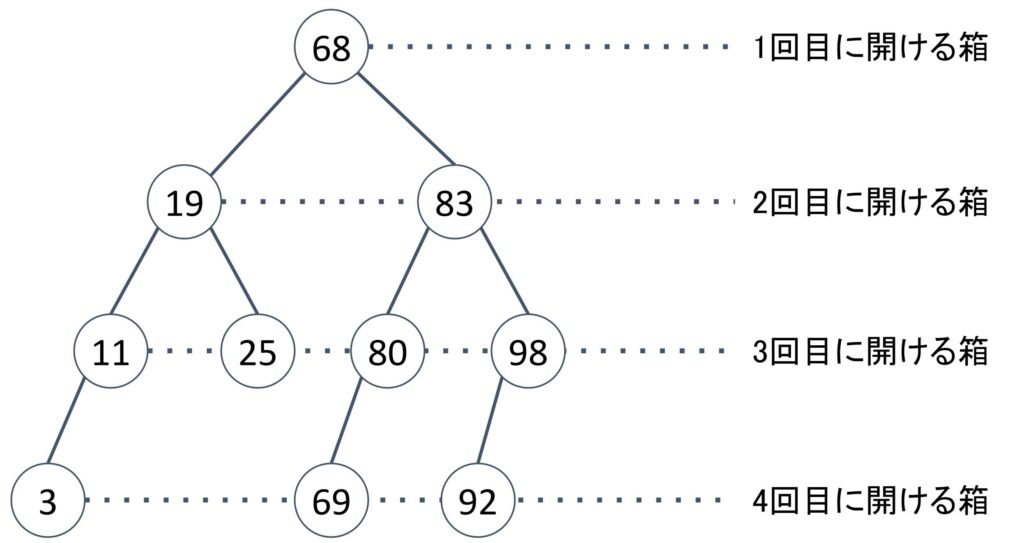
箱を開ける順番
2分探索木では2分探索で開ける箱がすぐに分かります。
68は全ての値の中央にある値なので、1回目に開ける箱になります。
また、19と83はそれぞれ【3,11,19,25】の中央にある値、【69,80,83,92,98】の中央にある値なので、2回目に開ける箱になります。
このように、2分探索木で上にある節の箱から開けていけば2分探索になると分かります。
AVL木
ちなみに、どの節においても左部分木と右部分木の深さの差が1以下の2分木をAVL木と呼びます。AVL木は左右のバランスが整っているため、AVL木になるようにデータを格納すると、効率的なデータの探索が可能になります。
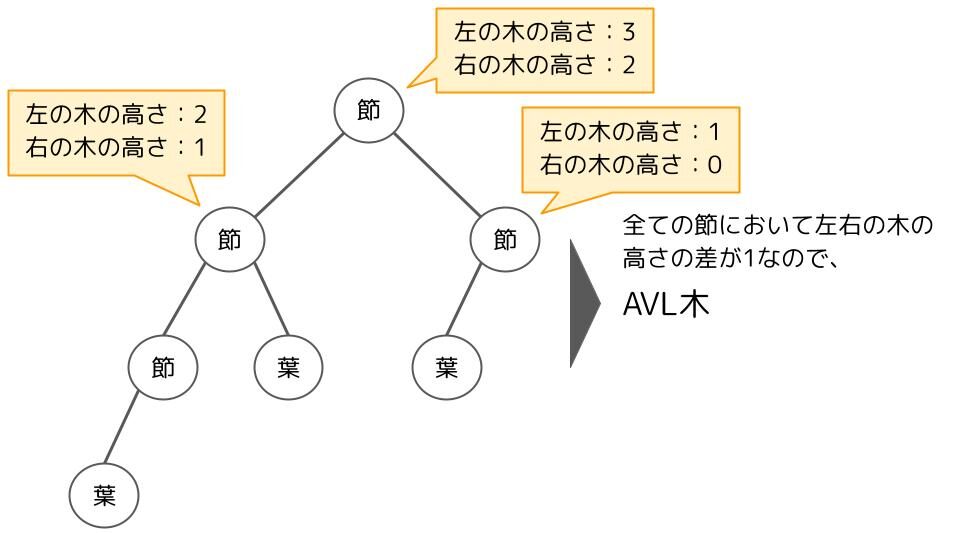
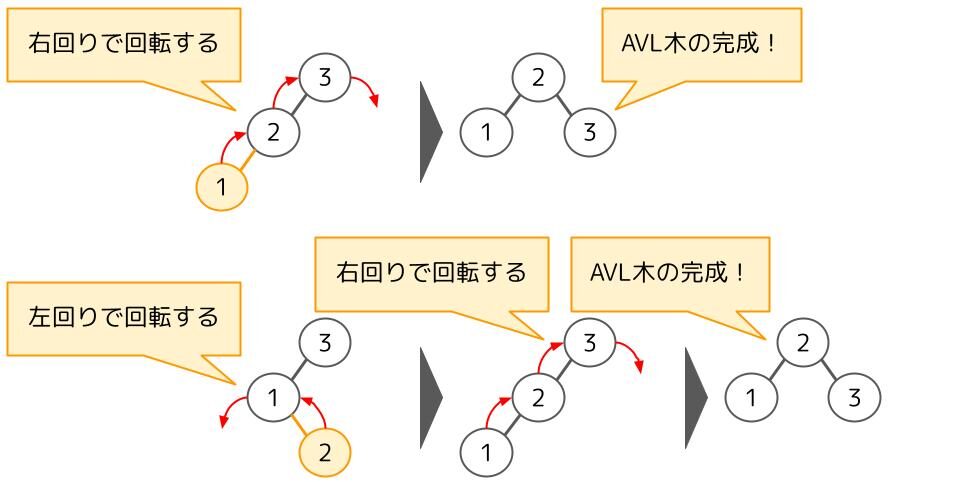
左右のバランスが取れていない2分探索木をAVL木にするためには回転という処理をします。例えば、左側の木が高い場合は次のような処理をします。右側の木が高い場合は逆回転ですね。
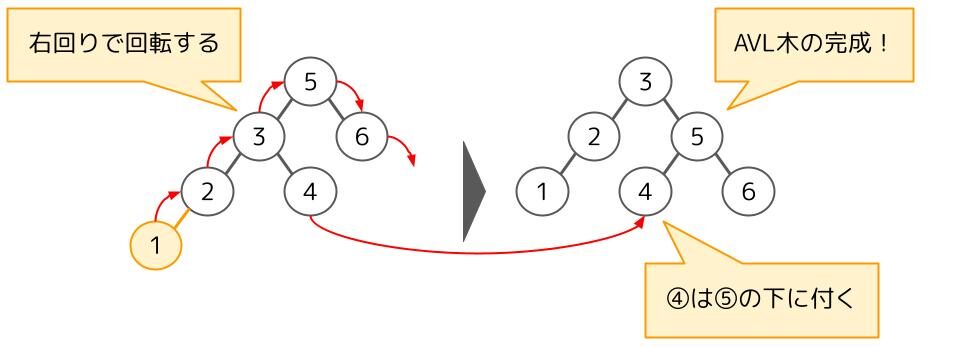
回転する部分は下の節から探していきます。下の2分探索木は③と④の節で左部分木と右部分木の深さの差が2以上になっています。この場合、③の方が下にあるので、③の節を中心に回転をします。
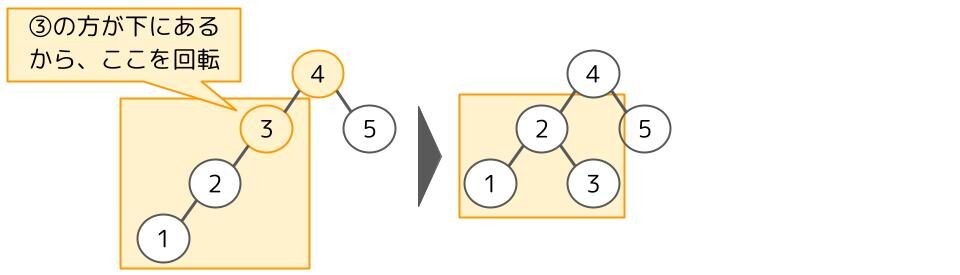
ハッシュ法
ハッシュ法とは、ハッシュ関数と言う「ある特定のルール」に従ってデータの格納場所を決めるやり方です。ハッシュ関数を使って求めた値をハッシュ値や関数値と言います。
下の例だと、数字「375」は配列の添字「75」に格納されます。

ハッシュ法を使えば、データがどこのアドレスに格納されているか一発で分かります。データを格納する配列がどれだけ大きくても一発で分かるので、配列の大きさとデータ検索に掛かる時間に関係性はありません。
しかし、問題点もあって、例えば「100で割った時の余りの数字のアドレスにデータを格納する」というルールだと「275」と「375」のハッシュ値は両方75になり、同じ場所に格納することになってしまいます。このように格納場所が重複してしまうことを衝突と言います。
応用情報技術者試験での出題例
令和7年度秋期問6
応用情報技術者
午前試験 令和7年度秋期問6
異なるn個のデータが昇順に整列された表がある。この表をm個のデータごとのブロックに分割し,各ブロックの最後尾のデータだけを線形探索することによって,目的のデータの存在するブロックを探し出す。次に,当該ブロック内を線形探索して目的のデータを探し出す。このときの平均比較回数を表す式はどれか。ここで,mは十分に大きく,nはmの倍数とし,目的のデータは必ず表の中に存在するものとする。
ア m+\(\displaystyle \frac{n}{m}\) イ \(\displaystyle \frac{m}{2}\)+\(\displaystyle \frac{n}{2m}\) ウ \(\displaystyle \frac{n}{m}\) エ \(\displaystyle \frac{n}{2m}\)
正解は”イ”
問題の表はこんな感じです。この表の場合、n=100、m=10となります。
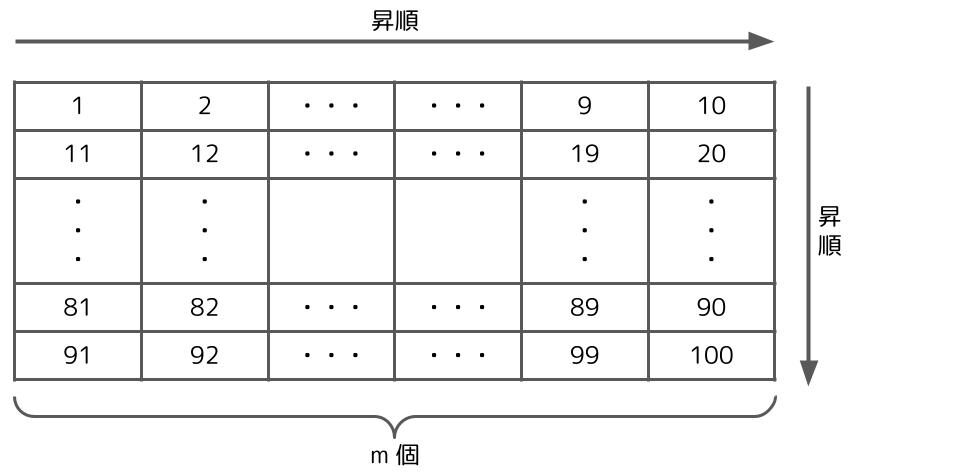
まず、各ブロックの最後尾のデータだけを線形探索します。探したい数字≦最後尾の数字なら、そのブロックの中に探したい数字があることが分かりますね。例えば、「12」を探す場合、最初に「10」と「12」を比較します。「12」は「10」よりも大きいので1行目のブロックには存在しないことが分かります。次に「20」と「12」を比較します。「12」は「20」よりも小さいので2行目のブロックに存在することが分かります。最後尾のデータは\(\displaystyle \frac{n}{m}\)個あり、最速で1個目、最遅で\(\displaystyle \frac{n}{m}\)個目に探したいブロックを見つけることが出来ます。
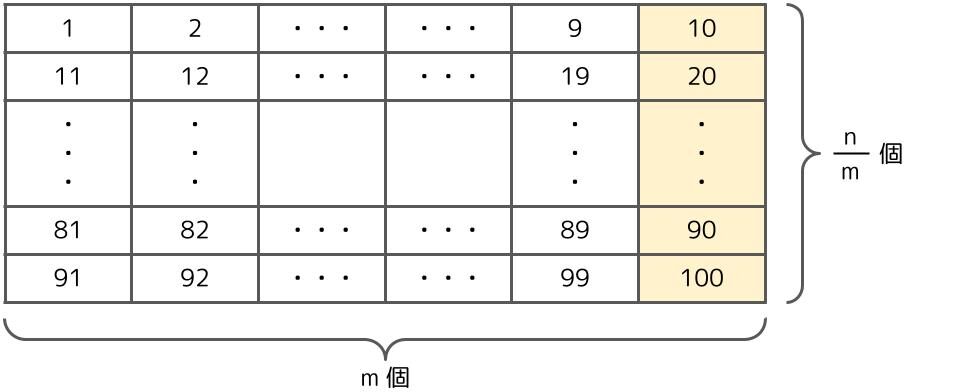
探したいブロックが分かれば、次は横方向に数字を探しに行きます。横方向の探索は、最速で1個に見つかり、最遅でm個目に見つかります。探したい数字が「11」なら1個目ですぐに見つかり、探したい数字が「20」なら10個目で見つかります。
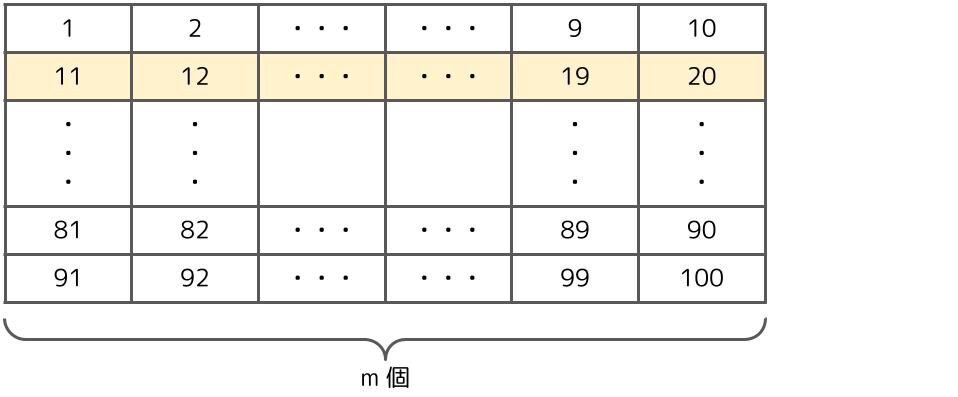
ここまでの探索をまとめてみましょう。
【縦方向の探索】
最速:1個目
最遅:\(\displaystyle \frac{n}{m}\)個目
【横方向の探索】
最速:1個目
最遅:m個目
よって、データが見つかる最速は2個目、最遅でm+\(\displaystyle \frac{n}{m}\)個目です。
なので、平均は(2+m+\(\displaystyle \frac{n}{m}\))÷2=1+\(\displaystyle \frac{m}{2}\)+\(\displaystyle \frac{n}{2m}\)となります。ただ、今回、mは十分に大きいため、最初の1は無視できます。10000回も10001回もほぼ同じじゃんってことですね。
よって、答えは\(\displaystyle \frac{m}{2}\)+\(\displaystyle \frac{n}{2m}\)でイとなります。
令和7年度春期問6
応用情報技術者
午前試験 令和7年度春期問6
図の2分探索木に1と0の二つの要素を順に追加したAVL木として,適切なものはどれか。
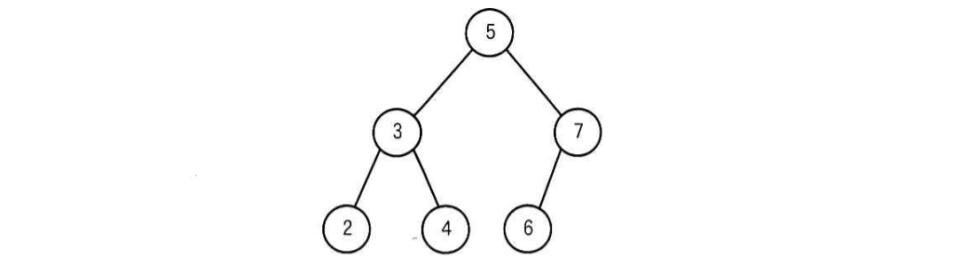
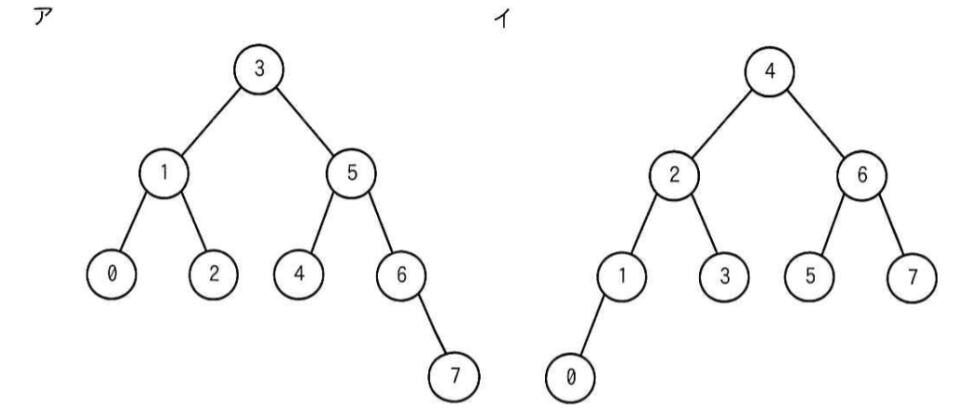
正解は”ウ”
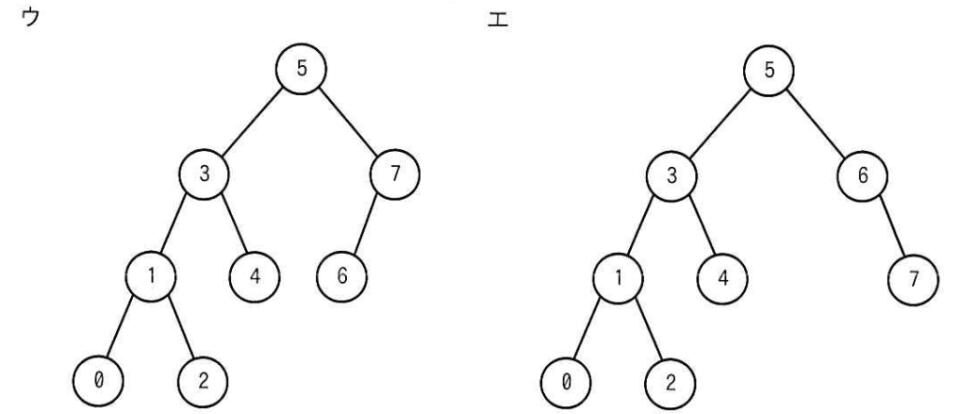
まずは「1」を追加しましょう。1は2よりも小さいので、2の左に1が付きます。この時点では、どの節(2、3、5、7)でも深さの差が1以下ですね。よって、これはAVL木です。
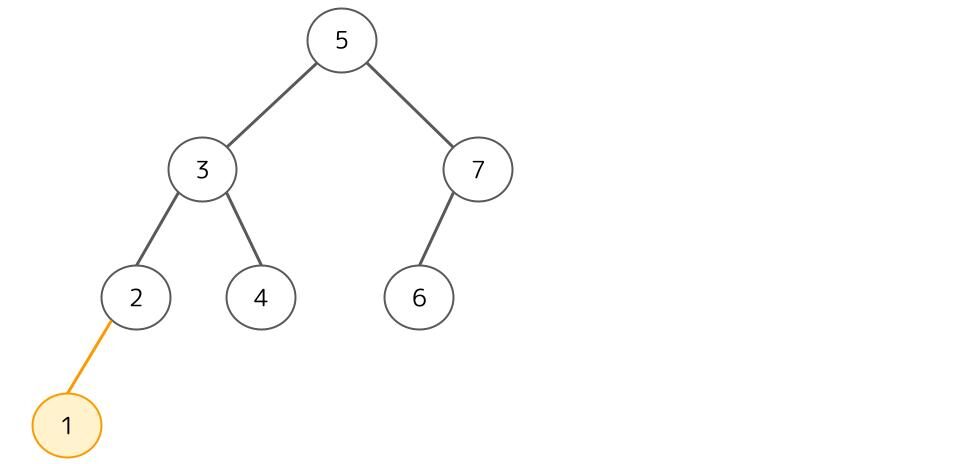
次に「0」を追加しましょう。0は1よりも小さいので1の左に0が付きます。
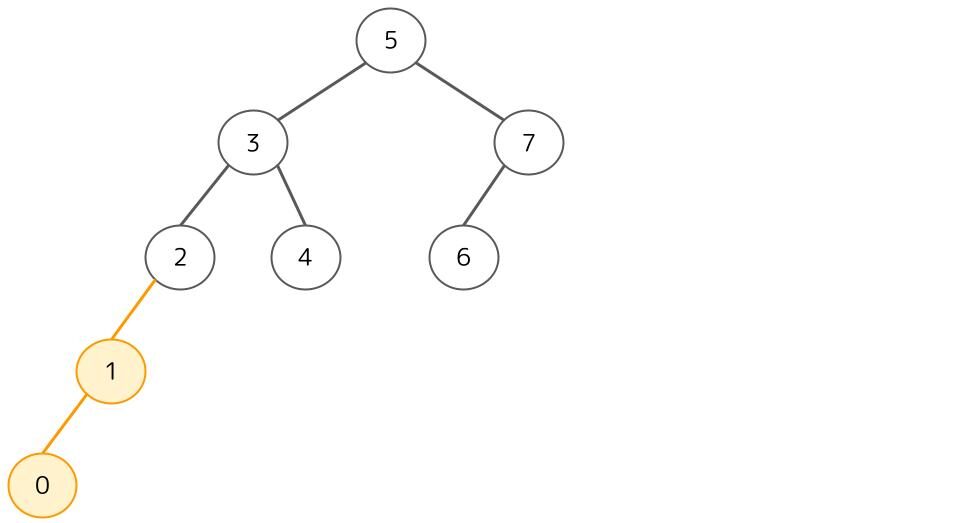
ここで②と③と⑤の左部分木と右部分木の深さの差が2以上になっています。この中で一番下の節は②なので、②を中心に回転します。
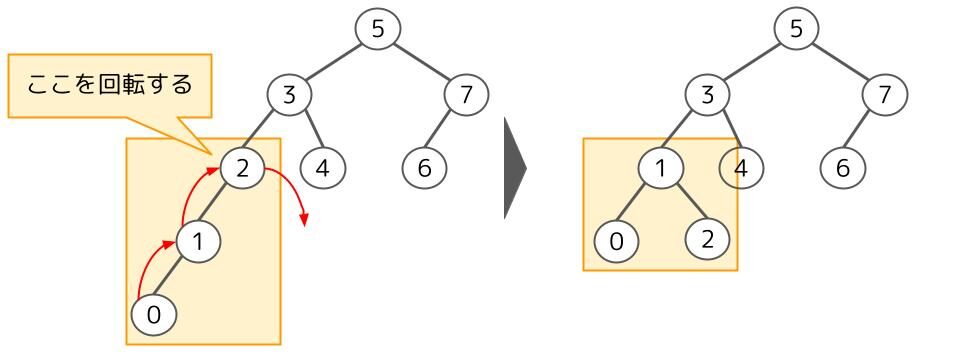
これでAVL木が完成しました。よって答えはウです。
令和6年度秋期問5
応用情報技術者
午前試験 令和6年度秋期問5
次の2分探索木から要素12を削除したとき,その位置に別の要素を移動するだけで2分探索木を再構成するには,削除された要素の位置にどの要素を移動すればよいか。
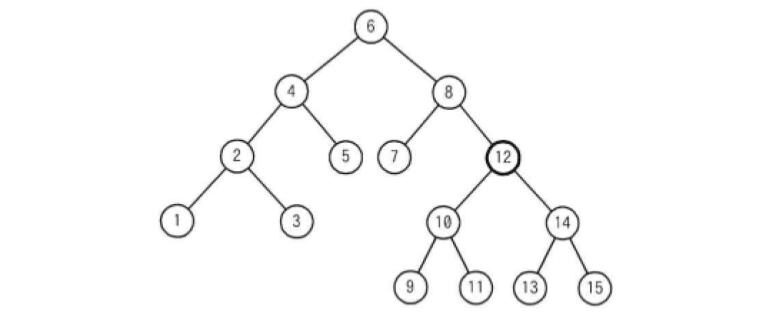
ア 9 イ 10 ウ 13 エ 14
正解は”ウ”
動かせる要素は1つだけなので、動かす可能性があるのは末端に位置する節(葉と言います)です。なので、1,3,5,7,9,11,13,15のどれかが答えです。
12の左の節には10、右の節には14があるので、12の代わりに入るのは10より大きく、14より小さい数字です。よって、答えは13ですね。
令和6年度秋期問6、令和4年度秋期問5
応用情報技術者
午前試験 令和6年度秋期問6、令和4年度秋期問5
自然数をキーとするデータを,ハッシュ表を用いて管理する。キーxのハッシュ関数h(x)を
h(x) = x mod n
とすると,任意のキーaとbが衝突する条件はどれか。ここで,nはハッシュ表の大きさであり,x mod nはxをnで割った余りを表す。
ア a+bがnの倍数
ウ nがa+bの倍数
イ a-bがnの倍数
エ nがa-bの倍数
正解は”イ”
衝突が起きるのは、aとbの格納場所が同じになる時です。
aとbをnで割り算した時に余りが同じになるのはa-bがnの倍数の時なので答えはイです。
(実際にやってみると)
a=17 b=10 n=7とすると、
aの格納場所:17÷7=2余り3
bの格納場所:10÷7=1余り3
で格納場所が被ります。この時、a-b=17-10=7で、これはnの倍数ですね。
令和5年度春期問5
応用情報技術者
午前試験 令和5年度春期問5
要求に応じて可変量のメモリを割り当てるメモリ管理方式がある。要求量以上の大きさをもつ空き領域のうちで最小のものを割り当てる最適適合(best-fit)アルゴリズムを用いる場合,空き領域を管理するためのデータ構造として,メモリ割当て時の平均処理時間が最も短いものはどれか。
ア 空き領域のアドレスをキーとする2分探索木
イ 空き領域の大きさが小さい順の片方向連結リスト
ウ 空き領域の大きさをキーとする2分探索木
エ アドレスに対応したビットマップ
正解は”ウ”
問題のメモリを図にすると次のような感じですね。

アやエのようにアドレスを使って探索しても最小の空き領域は見つかりません。空き領域を使って探索をするべきですね。
イのような片方向連結リストの場合は先頭から順に探索していきます。これよりウの2分探索木の方が速く見つかるので、答えはウです。
リストについてはこちらの記事で詳しく解説しています。

令和5年度春期問6
応用情報技術者
午前試験 令和5年度春期問6
従業員番号と氏名の対がn件格納されている表に線形探索法を用いて,与えられた従業員番号から氏名を検索する。この処理における平均比較回数を求める式はどれか。ここで,検索する従業員番号はランダムに出現し,探索は常に表の先頭から行う。また,与えられた従業員番号がこの表に存在しない確率をaとする。
ア \(\displaystyle \frac{(n+1)na}{2}\)
ウ \(\displaystyle \frac{(n+1)(1-a)}{2}\)+\(\displaystyle \frac{n}{2}\)
イ \(\displaystyle \frac{(n+1)(1-a)}{2}\)
エ \(\displaystyle \frac{(n+1)(1-a)}{2}\)+na
正解は”エ”
線形探索法では、前から順番に探索します。
与えられた従業員番号がこの表に存在しない場合
表に存在しないため、n件全部比較した上で見つかりませんでした、となります。
よって、表に存在しない時の平均比較回数はnaですね。
与えられた従業員番号がこの表に存在する場合
表に存在する場合、1件目に探したいデータがあることもあるし、n件目に探したいデータがあることもあります。ただ、1件目にデータがある確率とn件目にデータがある確率は同じですよね。なので、平均して丁度真ん中の\(\displaystyle \frac{(n+1)n}{2}\)回比較すれば良いと分かります。
例えば、11個の箱が並んでいて、前から順番に探していけば、平均して真ん中の6回目の比較で見つかりそうだと感覚的にイメージ出来ると思います。
よって、表に存在する時の平均比較回数は\(\displaystyle \frac{(n+1)(1-a)}{2}\)ですね。
よって、答えは、\(\displaystyle \frac{(n+1)(1-a)}{2}\)+naで、エとなります。
令和5年度春期問19
応用情報技術者
午前試験 令和5年度春期問19
ハッシュ表の理論的な探索時間を示すグラフはどれか。ここで,複数のデータが同じハッシュ値になることはないものとする。
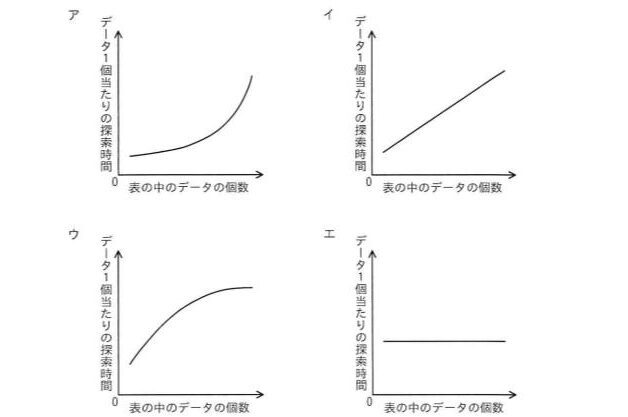
正解は”エ”
ハッシュ表とは、「元の値」と「元の値のハッシュ値」を対応付けて管理している表です。
元の値に対応するハッシュ値はただ一つしか存在しないので、表の中のデータの数が多くても、一発で探し当てることが可能です。よって、データの数に関係なく探索時間が変わらない、エが正解です。


