【応用情報】2進数と10進数をそれぞれ変換する方法について解説
この記事では、2進数を10進数に、10進数を2進数に変換する方法について、初心者にも分かりやすく、図解付きで丁寧に解説しています!
2進数
- 2進数は0と1だけで数字を表現する方法
2進数を10進数に変換する
- 2進数の各位の重みを足すと10進数になる。
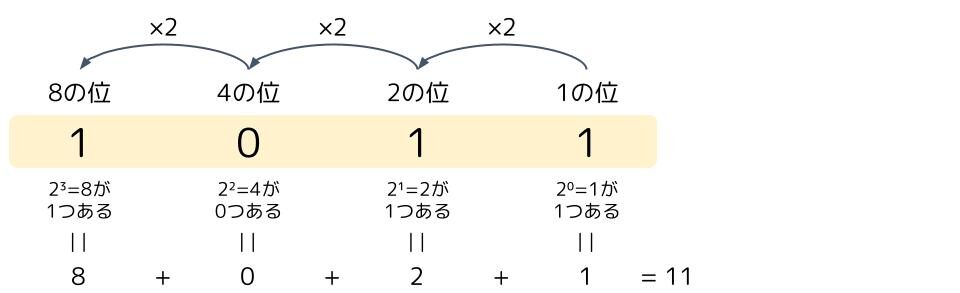
例えば、「1011」の場合は、8+2+1=11が10進数に変換した値になる。
10進数を2進数に変換する
- 10進数を2進数に変換するには、ひたすら2で割って余りを繋げる。
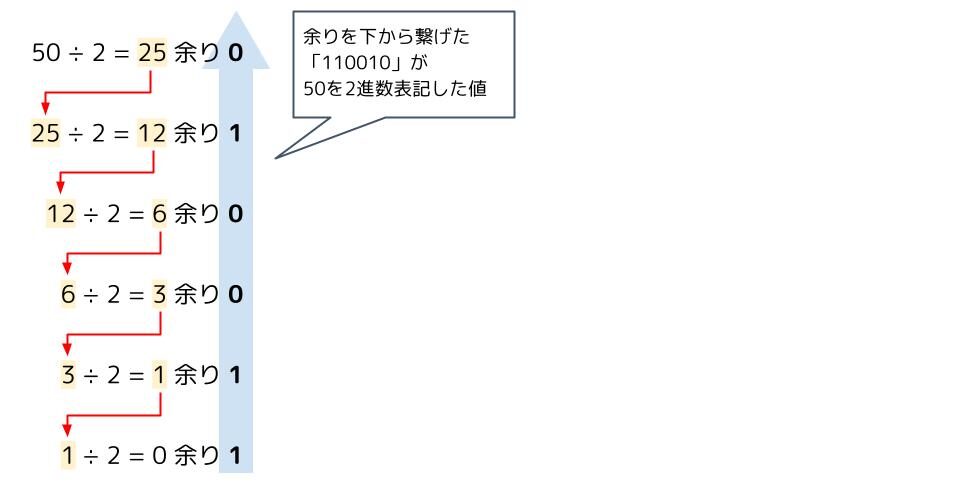
例えば、10進数「50」を2進数に変換すると「110010」になる。
2進数は0と1だけで数を数える方法
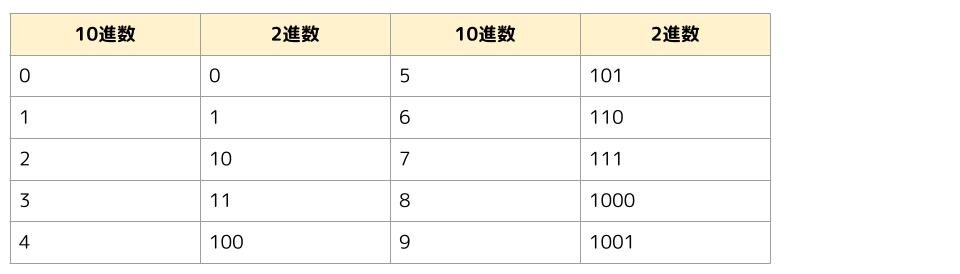
2進数とは「0」と「1」だけで数を表す方法です。
私たちが普段使う10進数では、0から9までの10個の数字で数を表します。
10進数では、「9」より1つ大きい数字は「10」になります。これは「9」より大きい1桁の数字が無いからですね。
同じように、2進数では「1」より1つ大きい数字は「10」になります。2進数で最も大きい1桁の数字は「1」だからです。
なぜコンピュータの勉強で2進数を学ぶのか
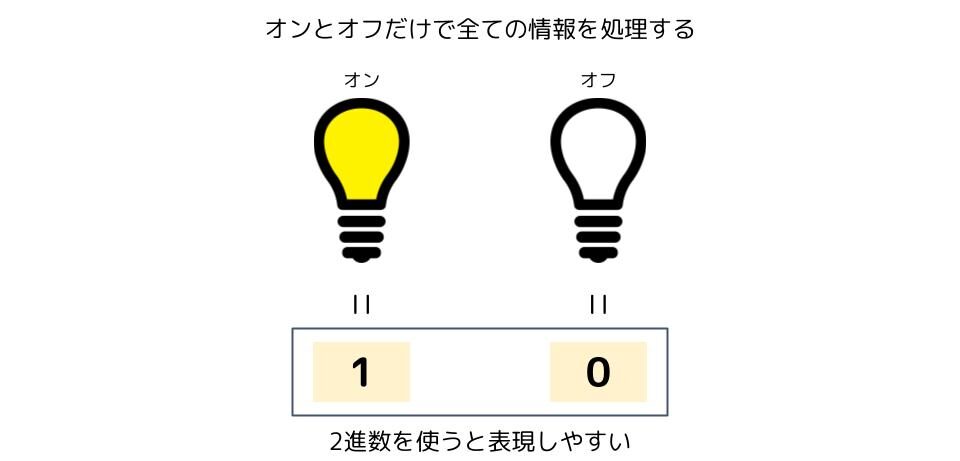
コンピュータは電子機器です。なので、電気を使って様々な処理をしています。
電気にはオンとオフの2つの状態しかありません。この2つの状態を「1」と「0」で表現するのが便利なので、「1」と「0」で数を表す2進数がコンピュータでは使われるという訳です。
2進数を10進数に変換する方法
2進数を10進数に変換する方法を学ぶ前提として、位取り記数法の考え方を知って欲しいと思います。難しい名前ですが、実は私たちは普段、位取り記数法で数を表現しています。
例えば、10進数で「2356」と記載があれば、1000が2つ、100が3つ、10が5つ、1が6つあることを表しています。位は10倍ずつ上がっていくので、右から4つ目の位は1000の位で、そこにある「2」は「2000」を意味すると無意識で理解しています。この考え方が位取り記数法です。
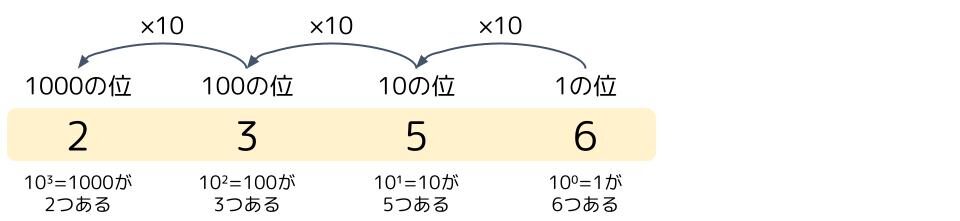
では、2進数の場合はどうなるでしょうか?
2進数の場合も同じように考えます。「1011」と記載があれば、8が1つ、4が0つ、2が1つ、1が1つあることを表しています。2進数の場合、位は2倍ずつ上がっていくので、右から4つ目の位は8の位で、そこにある「1」は「8×1=8」を意味します。同じように全ての桁の値を考えていくと、2進数の「1011」は10進数の「11」だと計算出来ます。これが2進数を10進数に変換する方法です。

10進数を2進数に変換する方法
10進数を2進数に変換するには、ひたすら2で割って余りを繋げます。
「50」を2進数に変換してみましょう。
- 「50」を2で割る。50÷2=25余り0
- ①の商である「25」を2で割る。25÷2=12余り1
- ②の商である「12」を2で割る。12÷2=6余り0
- ③の商である「6」を2で割る。6÷2=3余り0
- ④の商である「3」を2で割る。3÷2=1余り1
- ⑤の商である「1」を2で割る。1÷2=0余り1
- 商が「0」になったので2で割るのはここで終わり。
- 余りを下から繋げると「110010」となる。
これが「50」を2進数表記した値になる。

なぜ上の方法で10進数を2進数に変換出来るのか
「50」を2で割り続ける操作を図にしてみましょう。
「50÷2=25余り0」は50個の玉で2個1組のペアを作るとき、25個の箱が出来て、余りの玉が無いことを意味します。
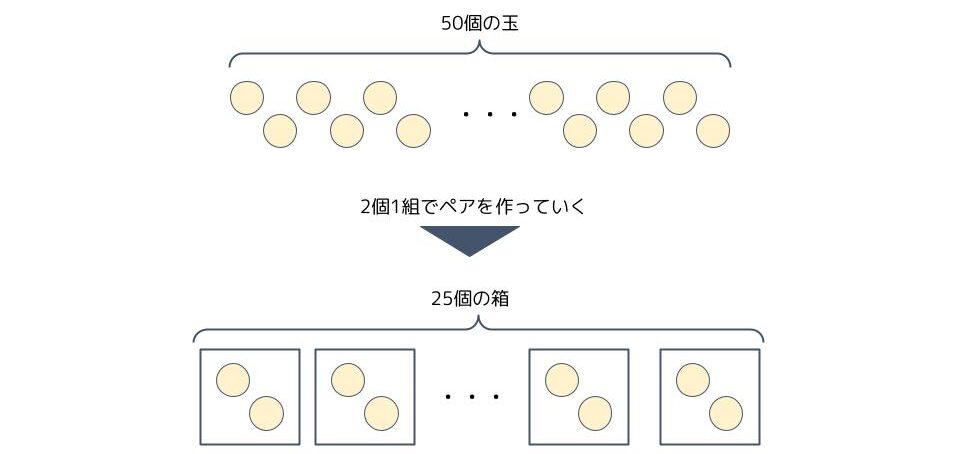
次の「25÷2=12余り1」は上で作った2個入りの箱で、更に2箱1組のペアを作るとき、12個の箱が出来て、1箱余ることを意味します。
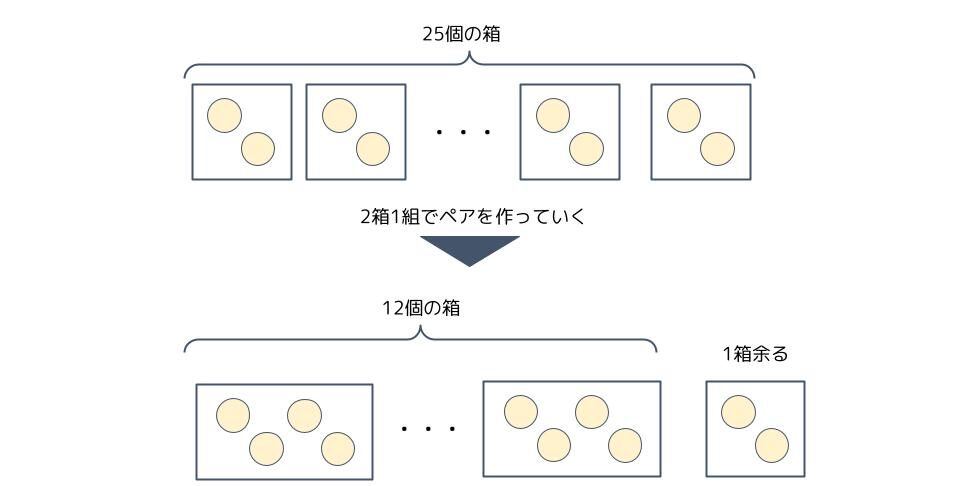
同じように、「12÷2=6余り0」は上で作った4個入りの箱で、更に2箱1組のペアを作るとき、6個の箱が出来て、余りの箱が無いことを意味し、
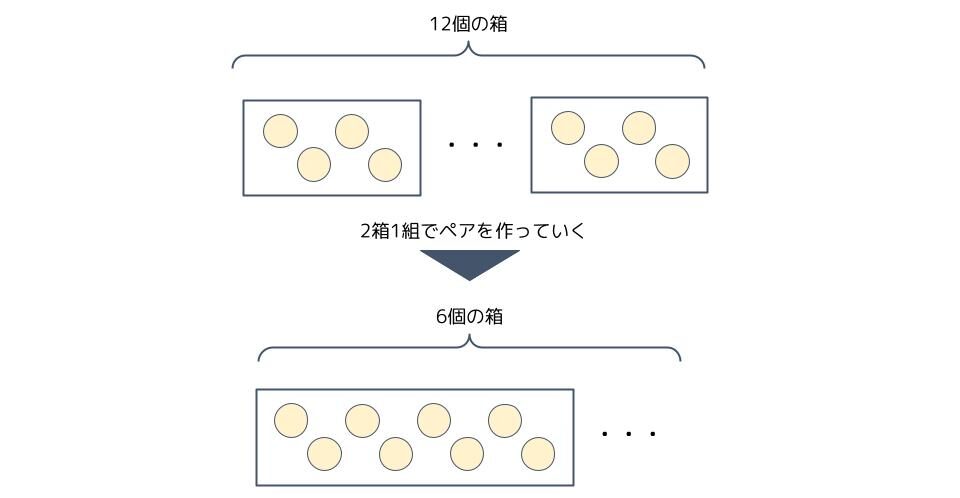
「6÷2=3余り0」は上で作った8個入りの箱で、更に2箱1組のペアを作るとき、3個の箱が出来て、余りの箱が無いことを意味し、
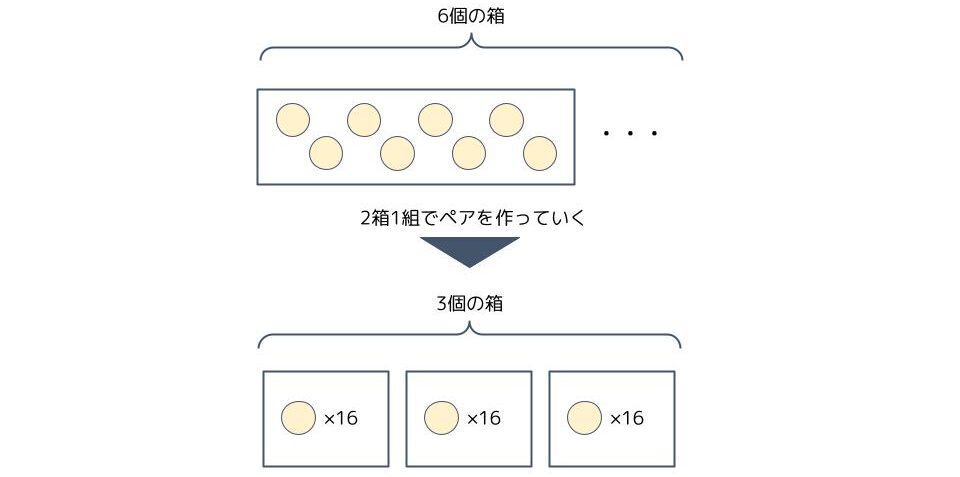
「3÷2=1余り1」は上で作った16個入りの箱で、更に2箱1組のペアを作るとき、1個の箱が出来て、1箱余ることを意味し、
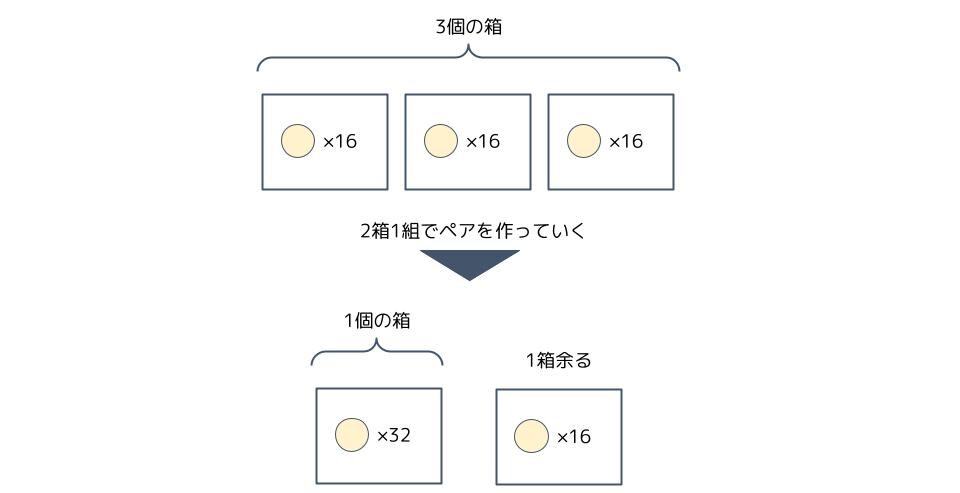
最後の「1÷2=0余り1」は上で作った32個入りの箱で、更に2箱1組のペアを作るとき、ペアは出来ずに、1箱余ることを意味します。
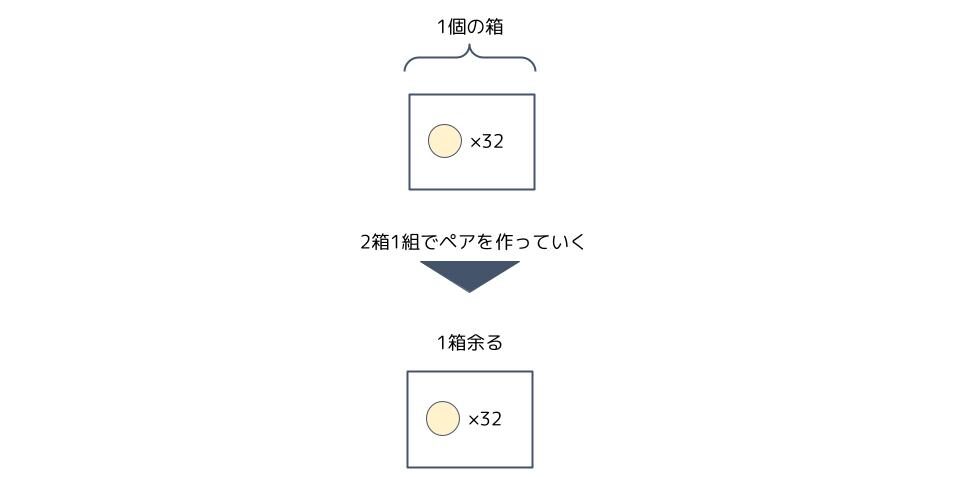
以上のことから、「50」個の玉をそれぞれの箱に振り分けていくと、
「32個入りの箱」が1箱、「16個入りの箱」が1箱、「8個入りの箱」が0箱、
「4個入りの箱」が0箱、「2個入りの箱」が1箱、玉の余りが出ないことが分かりました。
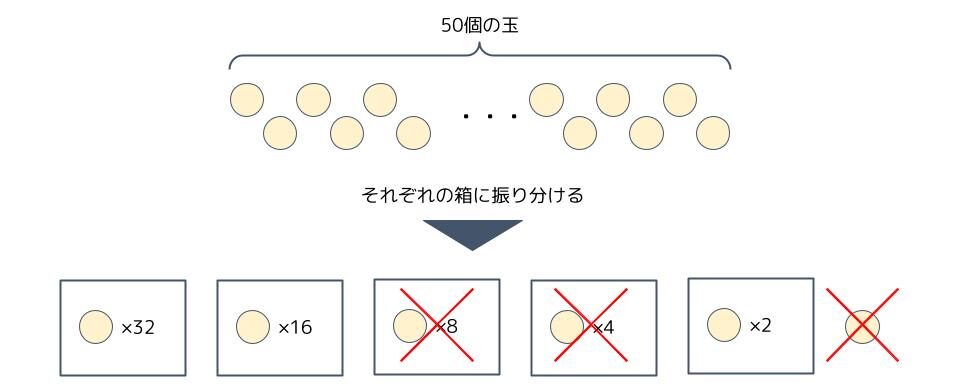
2進数の数字の各桁は、それぞれ各位の値が何個あるのかを表していました。
なので、上の箱はこう表すことも出来ますよね。

これで、「50」を2進数で表記することが出来ました。
今回の内容について、Youtubeでも解説しています。動画で学びたい!って人は是非見てみてください!
応用情報技術者試験での出題例
令和5年度秋期問1
応用情報技術者
午前試験 令和5年度秋期問1
2桁の2進数x₁x₂が表す整数をxとする。2進数x₂x₁が表す整数を,xの式で表したものはどれか。ここで,int(r)は非負の実数rの小数点以下を切り捨てた整数を表す。
ア 2x + 4int(\(\displaystyle \frac{x}{2}\))
ウ 2x - 3int(\(\displaystyle \frac{x}{2}\))
イ 2x + 5int(\(\displaystyle \frac{x}{2}\))
エ 2x - 4int(\(\displaystyle \frac{x}{2}\))
正解は”ウ”
2進数x₁x₂を「10」とすると、整数x=2で、
2進数x₂x₁は「01」となり、これの整数は1です。
実際にア~エの選択肢にx=2を代入してみましょう。
ア 2x + 4int(\(\displaystyle \frac{x}{2}\))=2×2+4int(1)=8
イ 2x + 5int(\(\displaystyle \frac{x}{2}\))=2×2+5int(1)=9
ウ 2x - 3int(\(\displaystyle \frac{x}{2}\))=2×2-3int(1)=1
エ 2x - 4int(\(\displaystyle \frac{x}{2}\))=2×2-4int(1)=0
答えが1になったのはウだけなので、答えはウだと分かります。
令和4年度秋期問1
応用情報技術者
午前試験 令和4年度秋期問1
aを正の整数とし,b=a²とする。aを2進数で表現するとnビットであるとき,bを2進数で表現すると最大で何ビットになるか。
ア n+1 イ 2n ウ n² エ 2ⁿ
正解は”イ”
aが2ビットの場合
aが2ビットの場合、aの最大値は「11」、整数で表すと「3」です。
このとき、b=9となり、2進数で表すと「1001」となります。
よって、aが2ビットの場合、bを2進数で表現すると最大で4ビットになります。
aが3ビットの場合
aが3ビットの場合、aの最大値は「111」、整数で表すと「7」です。
このとき、b=49となり、2進数で表すと「110001」となります。
よって、aが3ビットの場合、bを2進数で表現すると最大で6ビットになります。
aが4ビットの場合
aが4ビットの場合、aの最大値は「1111」、整数で表すと「15」です。
このとき、b=225となり、2進数で表すと「11100001」となります。
よって、aが4ビットの場合、bを2進数で表現すると最大で8ビットになります。
aが2ビットの場合、最大で4ビット
aが3ビットの場合、最大で6ビット
aが4ビットの場合、最大で8ビット
なので、aがnビットの場合、最大で2nビットが成り立ちます。
よって、答えはイです。



