【応用情報】初心者向け!集合と命題について解説!
この記事では、集合と命題について、初心者にも分かりやすく、図解付きで丁寧に解説しています!
集合
- 集合は何かの集まりのことで、集合同士の関係性を分かりやすく図示したものをベン図と呼ぶ。
- 積集合は2つの集合の共通する部分。
- 和集合は2つの集合を合わせた部分。
- 補集合は特定の集合に合致しない部分。
- 差集合は片方の集合からもう片方の集合を引いた部分。
命題
- 命題は誰が見ても正しいか正しくないかを判断できる文章や式
集合
集合とはその名の通り、何かの集まりのことです。集合に属する一つ一つのモノを要素と呼びます。
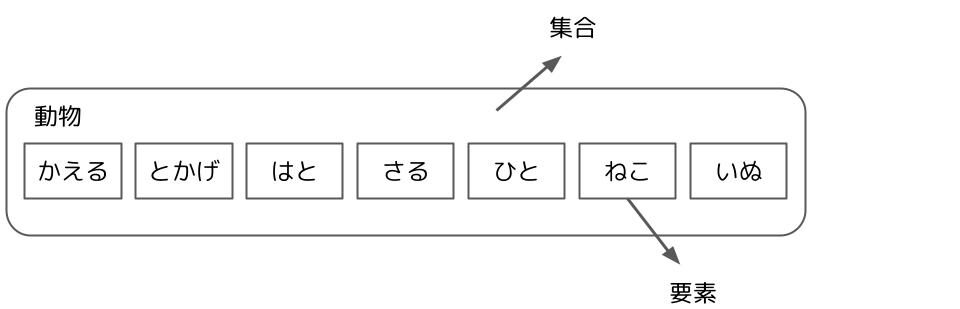
集合の中に、更に小さな集合があります。「動物」の中には「哺乳類」がいます。このように、集合に含まれる小さな集合を部分集合と呼びます。

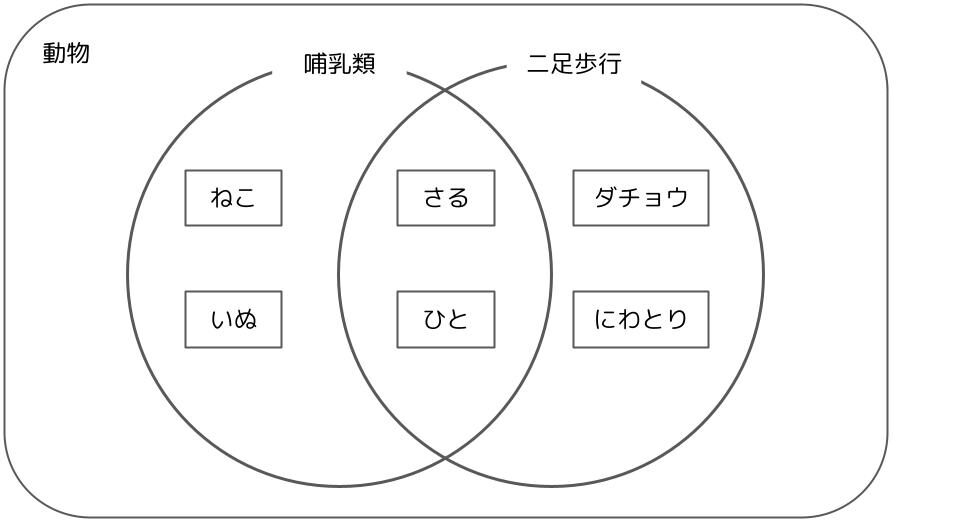
部分集合と部分集合の関係性を分かりやすく表した図をベン図と呼びます。例えば、「哺乳類」と「2足歩行」という部分集合があるベン図はこうなります。哺乳類の要素は{ねこ,いぬ,さる,ひと}、二足歩行の要素は{さる,ひと,ダチョウ,にわとり}で、それぞれ部分集合の円の中に入っています。{さる,ひと}は哺乳類でもあり二足歩行でもあるので、両方の円が重なる部分に入ります。
集合演算
集合演算とは複数の集合に対して演算を行うことで、集合同士で重なっている箇所を抽出したり、異なる箇所を抽出できます。
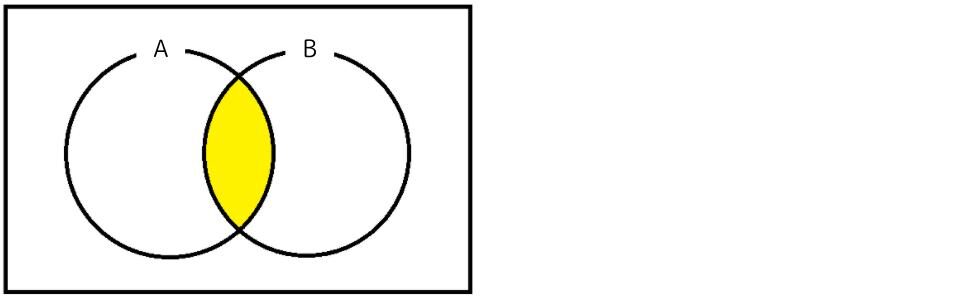
積集合(共通演算)
2つの集合の両方に含まれる箇所です。Aでもあり、Bでもある箇所ですね。「A∩B」と表します。
和集合
2つある集合を合わせた箇所です。AまたはBである箇所ですね。「A∪B」と表します。

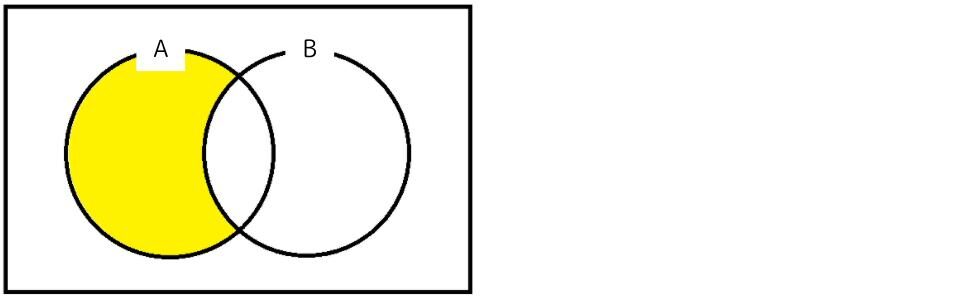
補集合
ある集合に合致しない箇所です。Aではない箇所ですね。「A」と表します。

差集合
片方の集合からもう片方の集合を引いた箇所です。AだけどBではない箇所ですね。「AーB」と表します。
命題
命題とは誰が見ても正しいか正しくないかを判断できる文章や式のことです。「100は5よりも大きい」とか「6<1」とかですね。命題の答えは「True(真)」か「False(偽)」になります。命題が正しければTrueで、間違えていればFalseです。
例えば「100は5よりも大きい」は正しいので、答えは「True(真)」になります。「6<1」は間違えているので、答えは「False(偽)」になります。
また、命題には含意という考え方もあります。2つの命題AとBがあったとき、「AならばB」は成り立つのか?という考え方です。含意は以下の4つが成り立ちます。
- 命題AがTrue、命題BがTrueのとき、「AならばB」は成り立つ(True)
- 命題AがTrue、命題BがFalseのとき、「AならばB」は成り立たない(False)
- 命題AがFalse、命題BがTrueのとき、「AならばB」は成り立つ(True)
- 命題AがFalse、命題BがFalseのとき、「AならばB」は成り立つ(True)
この4つをまとめたものが下の表です。「AならばB」は「A→B」と表現しています。
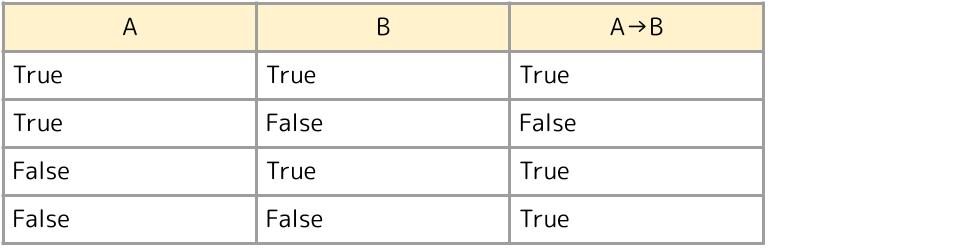
これだけだと分かりにくいので例を見てみましょう。雨が降ると絶対に家から出ない人がいます。
命題A:雨が降っている
命題B:彼は家に居る
命題AがTrue、命題BがTrueのとき、A→Bは「雨が降っている、ならば、彼は家に居る」となります。これは正しいのでTrueですね。
命題AがTrue、命題BがFalseのとき、A→Bは「雨が降っている、ならば、彼は家に居ない」となります。これは正しくないのでFalseですね。
命題AがFalse、命題BがTrueのとき、A→Bは「雨が降っていない、ならば、彼は家に居る」となります。これが哲学的で難しいのですが、「雨が降ると絶対に家から出ない」がルールなので、雨が降っていないときは家に居ても居なくてもどっちでも良いんですね。なので、「雨が降っていない、ならば、彼は家に居る」は正しく、Trueとなります。
命題AがFalse、命題BがFalseのとき、A→Bは「雨が降っていない、ならば、彼は家にいない」となります。これも上と同じで正しいのでTrueとなります。
よって、この表が成り立つんですね。

応用情報技術者試験での出題例
令和7年度春期問1
応用情報技術者
午前試験 令和7年度春期問1
論理式P,Qがいずれも真であるとき,論理式Rの真偽にかかわらず真になる式はどれか。ここで,””は否定を,”∨”は論理和を,”∧”は論理積を,”→”は含意(”真→偽”となるときに限り偽となる演算)を表す。
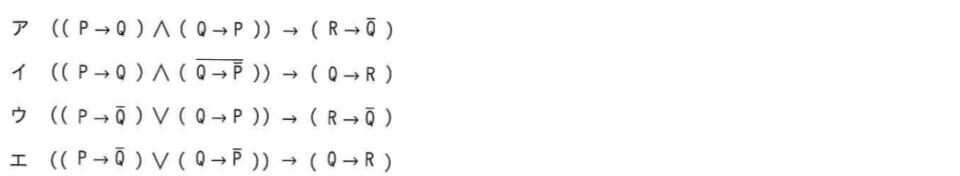
正解は”エ”
『”→”は含意(”真→偽”となるときに限り偽となる演算)を表す』と問題文に書いています。と言うことは、以下が成り立ちます。
- ”真→真”となるとき真となる
- ”真→偽”となるとき偽となる
- ”偽→真”となるとき真となる
- ”偽→偽”となるとき真となる
さて、選択肢を1つずつ見ていきましょう。
アはRが偽のとき、偽になります。よって、×です。

イはRが偽のとき、偽になります。よって、×です。

ウはRが偽のとき、偽になります。よって、×です。

エはRが真のときも偽のときも真になります。Rが真のときはこんな感じです。

Rが偽のときはこんな感じになります。

Rが真でも偽でも、論理式は真になるので、答えはエです。
令和7年度春期問28
応用情報技術者
午前試験 令和7年度春期問28
和両立である関係RとSがある。R∩Sと等しいものはどれか。ここで,ーは差演算,∩は共通演算を表す。
ア (RーS)ー(SーR)
ウ Rー(SーR)
イ Rー(RーS)
エ Sー(RーS)
正解は”イ”
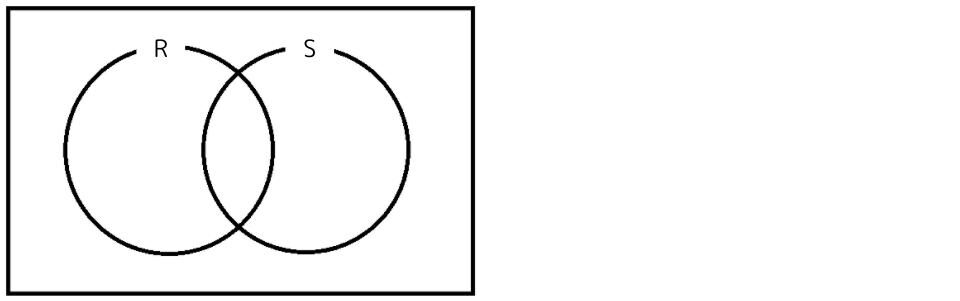
R∩Sをベン図で表すと下図になります。
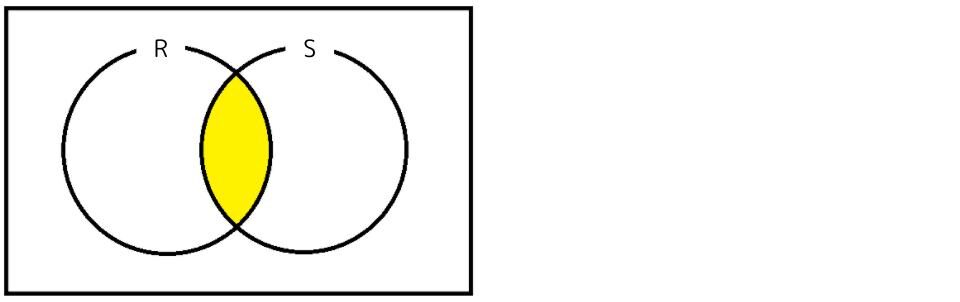
選択肢に出てくる「RーS」をベン図で表すと下図になります。「RだけどSではない部分」ですね。
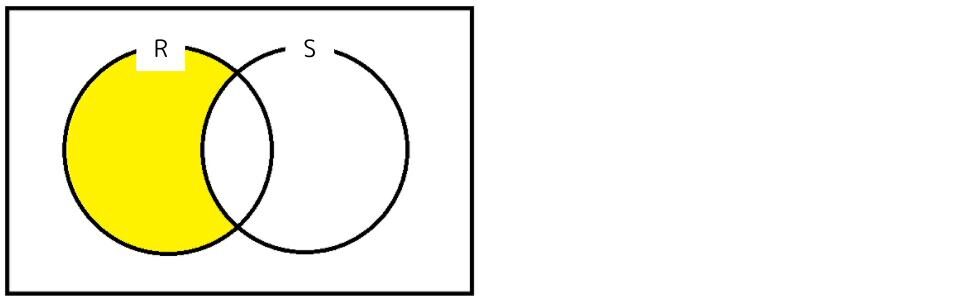
「SーR」のベン図は下図の通りです。「SだけどRではない部分」ですね。

さて、それぞれの選択肢を見てみましょう。
ア (RーS)だけど(SーR)ではない部分です。そんな部分はありませんね。なので、アの選択肢をベン図で表すとこうなります。
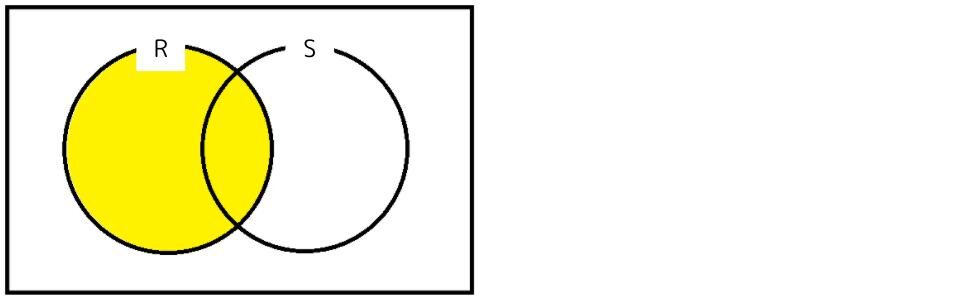
イ Rだけど(RーS)ではない部分です。ベン図で表すとこうなります。R∩Sと同じですね。よってイが正解です。

ウ Rだけど(SーR)ではない部分です。Rと(SーR)に被ってる部分はありません。なので、ウはRと全く同じになります。ベン図で表すとこうなります。
エ Sだけど(RーS)ではない部分です。Sと(RーS)に被ってる部分はありません。なので、ウはSと全く同じになります。ベン図で表すとこうなります。

令和4年度春期問2
応用情報技術者
午前試験 令和4年度春期問2
全体集合S内に異なる部分集合AとBがあるとき,A∩Bに等しいものはどれか。ここで,A∪BはAとBの和集合,A∩BはAとBの積集合,AはSにおける補集合,AーBはAからBを除いた差集合を表す。
ア AーB
イ (A∪B)ー(A∩B)
ウ (SーA)∪(SーB)
エ Sー(A∩B)
正解は”ア”
A∩Bをベン図で表すと下図になります。AでもないしBでもない部分ですね。

さて、それぞれの選択肢を見てみましょう。
ア AだけどBではない部分です。アの選択肢をベン図で表すとこうなります。A∩Bと同じなので、答えはアですね。

イ まず、(A∪B)はここです。Aではない部分、または、Bではない部分ですからね。

つぎに、(A∩B)はここです。AでもBでもある部分ですね。

よって、(A∪B)ー(A∩B)はここになります。

ウ まず、SーAはここです。

つぎに、SーBはここです。

よって、(SーA)∪(SーB)はここになります。

エ まず、A∩Bはここです。

よって、Sー(A∩B)はここになります。

以上から答えはアだと分かりますね。



