この記事ではM/M/1の待ち行列モデルについてIT初心者にも分かりやすく解説します。
M/M/1の待ち行列モデル
- M/M/1の待ち行列モデルは、1列に並んだ人やモノを1つの窓口やサーバが処理する時に、平均してどれくらいの時間待つのかを計算するための考え方。
- 平均利用率は処理能力に対して、実際どれだけ処理するかを表す率。
- 平均待機数は、平均して並んでいる人の数で、
平均待機数=平均利用率/(1-平均利用率)で表される。 - 平均待ち時間=平均待機数×平均サービス時間で表される。
応用情報ではM/M/1の待ち行列モデルに関する問題が出ます。是非最後までご覧ください。
M/M/1の待ち行列モデル
M/M/1の待ち行列モデルは、ATMや病院などでどれくらいの時間待つのか？を計算する方法です。M/M/1の待ち行列モデルは、1列に並んだ人やモノを1つの窓口やサーバが処理する場合に使うことが出来ます。
M/M/1の待ち行列モデルでは、待ち時間を次の式で表します。
平均待ち時間=平均待機数×平均サービス時間
=(平均利用率/1-平均利用率)×平均サービス時間
この式はどういう意味なのか。ATMを例に見てみましょう。
このATMを使う人達は、ATMの操作を始めてから完了するまでに平均3分要します。
つまり、このATMは1時間当たり20人を捌く能力があります。
また、このATMには1時間当たり5人来ます。
では、このATMは処理能力に対してどれくらい使われているのでしょうか？
処理能力に対してどれくらい使われているか
特定の時間内で処理できる人の数を平均サービス率、やってくる人の数を平均到着率と言います。このATMの平均サービス率と平均到着率は次のようになります。
- 1時間で20人処理できる → 平均サービス率=20人/時間
- 1時間で5人やってくる → 平均到着率=5人/時間
ここから平均利用率を計算してみましょう。平均利用率とは、処理能力に対して実際にどれくらい使われているかを示した値です。
1時間で20人処理できるATMに対して5人来たので、当たり前ですが、ATMはこの1時間で5人処理していますね。また、ATMは1時間で20人の人を処理できる処理能力を持っているので、平均利用率は次のようになります。
平均利用率=5人÷20人=0.25
つまり、ATMの処理能力に対して1/4使われていることが分かります。
では、このATMは平均してどれくらい待つのでしょうか。
行列に並ぶ時間を計算する
行列に並ぶ時間の平均値を平均待ち時間、行列に並ぶ人の平均値を平均待機数と呼び、平均待ち時間は次の式で表せます。
なお、平均サービス時間はATMが1人処理するのに掛かる平均的な時間です。
平均待機数=平均利用率/1-平均利用率
平均待ち時間=平均待機数×平均サービス時間
平均待機数がなぜこの式になるのかを説明するには、微分や確率論といった難しい数学の話をしないといけないので、ここでは感覚的に分かるようにざっくり説明したいと思います。
平均利用率は、処理能力に対してどれくらい使われているかを示す値で、ATMの平均利用率は0.25でした。と言うことは、処理能力に対してどれくらい使われていないかを示す「平均利用されていない率」は0.75ですね(平均利用されていない率は私が適当に作った言葉です）。ここから平均待機数を計算してみましょう。
平均待機数(並ぶ人)×平均利用されていない率
= 平均利用数(利用する人)×平均利用率
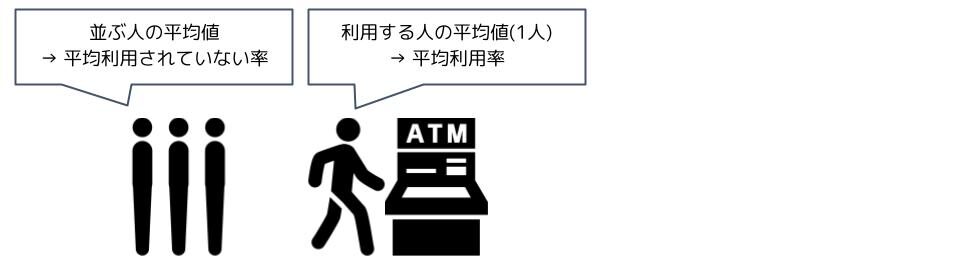
ここで、平均利用されていない率=1-平均利用率で、M/M/1行列では利用する人=1人でした。よって、平均待機数が次の式で表されることが分かります。
平均待機数×(1-平均利用率)=1×平均利用率
つまり、
平均待機数=平均利用率/1-平均利用率
待ち時間は待っている人の数×ATMに掛かる時間なので、次の式で表されます。
平均待ち時間=平均待機数×平均サービス時間
応用情報技術者試験での出題例
令和6年度秋期問1、令和4年度春期問3
応用情報技術者
午前試験 令和6年度秋期問1、令和4年度春期問3
M/M/1の待ち行列モデルにおいて，窓口の利用率が25%から40%に増えると，平均待ち時間は何倍になるか。
ア 1.25
ウ 2.00
イ 1.60
エ 3.00
正解は”ウ”
平均待ち時間は次の式で表せます。
平均待ち時間=(平均利用率/1-平均利用率)×平均サービス時間
利用率が25%のとき
平均待ち時間=\(\displaystyle \frac{0.25}{1-0.25}\)×平均サービス時間=\(\displaystyle \frac{1}{3}\)×平均サービス時間
利用率が40%のとき
平均待ち時間=\(\displaystyle \frac{0.4}{1-0.4}\)×平均サービス時間=\(\displaystyle \frac{2}{3}\)×平均サービス時間
よって答えは2倍となります。
令和6年度春期問2、令和3年度秋期問2
応用情報技術者
午前試験 令和6年度春期問2、令和3年度秋期問2
ATM(現金自動預払機)が1台ずつ設置してある二つの支店を統合し，統合後の支店にはATMを1台設置する。統合後のATMの平均待ち時間を求める式はどれか。ここで，待ち時間はM/M/1の待ち行列モデルに従い，平均待ち時間にはサービス時間を含まず，ATMを1台に統合しても十分に処理できるものとする。
〔条件〕
(1):平均サービス時間:Ts
(2):統合前のシステムの利用率:両支店ともρ
(3):統合後の利用者数は，統合前の両支店の利用者数の合計
ア (\displaystyle \frac{ρ}{1-ρ}\)×Ts
イ (\displaystyle \frac{ρ}{1-2ρ}\)×Ts
ウ (\displaystyle \frac{2ρ}{1-ρ}\)×Ts
エ (\displaystyle \frac{2ρ}{1-2ρ}\)×Ts
正解は”エ”
平均待ち時間と平均利用率は次の式で表せます。
- 平均待ち時間=(平均利用率/1-平均利用率)×平均サービス時間
- 平均利用率 =平均到着率/平均サービス率
平均サービス率は「特定の時間内で処理できる人の数」で、
平均到着率は「特定の時間内でやってくる人の数」を表します。
支店の統合後、平均到着率は2倍になりますが、平均サービス率は変わりません。
よって、平均利用率は統合前の2倍の2ρになります。
なので、平均待ち時間は(\displaystyle \frac{2ρ}{1-2ρ}\)×Tsとなります。
