応用情報技術者ではそこそこの頻度でM/M/1の待ち行列モデルに関する問題が出題されます。ここでマスターしましょう。

M/M/1の待ち行列モデル
そもそもM/M/1の待ち行列モデルとは、次のようなことを考えるときに使われます。
ある処理能力を持ったシステムに、どんどん命令が送られたとき、
どれくらいの速さで命令を処理できるのか?
会社に設置したプリンターを例に見てみましょう。
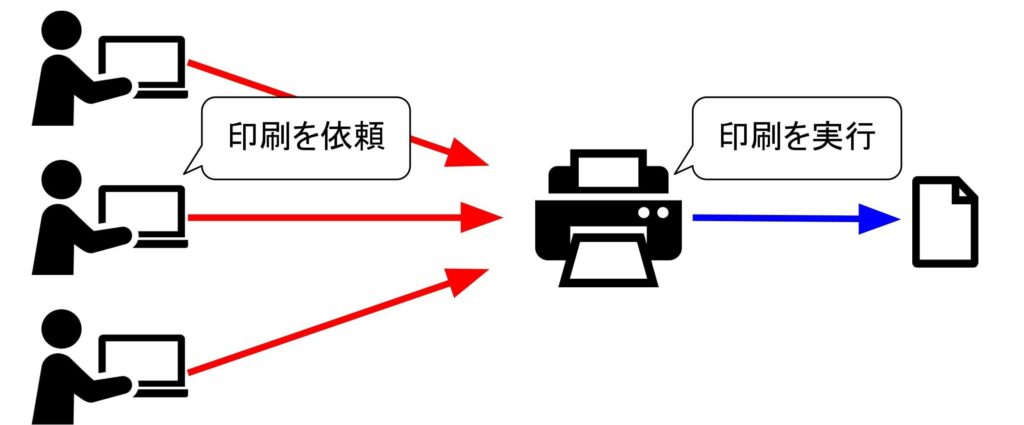
社員は会社に設置されたプリンターで印刷を行います。
忙しい時間帯ならプリンターの処理能力以上の印刷依頼が届き、待ち時間が発生します。
逆に、人が少ない朝はプリンターに余裕が出来て、待ち時間が発生することなく印刷が出来ます。
ここで大切なのは、時間帯によって依頼件数が異なるし、プリンターの処理能力以上に印刷依頼が来ることもあるということです。
では、プリンターは平均してどれくらい利用されていたのでしょうか?
平均利用率
平均利用率とは、処理能力に対してどれだけ依頼件数があったのかを表す指標です。
平均利用率の公式
平均利用率は平均サービス率と平均到着時間を用いて次の式で表すことが出来ます。
平均利用率 = 平均到着率 ÷ 平均サービス率
平均サービス率:ある時間の中で何件の依頼を実行できるのか
平均到着率 :ある時間の中で何件の依頼が来るのか
ここではある時間を1時間としましょう。
平均利用率 = 平均到着率 ÷ 平均サービス率の公式は、1時間プリンターが処理している間に何件の依頼が到着するかの割合を表していることが分かります。
具体例
プリンターを1日観察すると、下のような状況だと分かりました。
- 処理能力:プリンターは1日に12000件の印刷をする能力がある。
- 依頼件数:1日に7200件の印刷依頼が届いていた。
すると、平均サービス率と平均到着率は次のようになります。
- 平均サービス率 = 12000件 ÷ 24時間 = 500件/時間
- 平均到着率 = 7200件 ÷ 24時間 = 300件/時間
つまり、プリンターが1時間で500件印刷している間に300件の印刷依頼が到着しているということです。なので、平均利用率は次の式で求めることが出来ます。
平均利用率 = 300 ÷ 500 = 0.6
プリンターの処理能力に対して平均60%の依頼が到着していたということが分かります。
平均待機数
まず、平均でどれだけの依頼が待機しているのかを求めます。
平均待機数 = 平均利用率/(1-平均利用率)
少し分かりにくいですが、平均待機数は印刷待ちの依頼と印刷中の依頼を合計した値です。
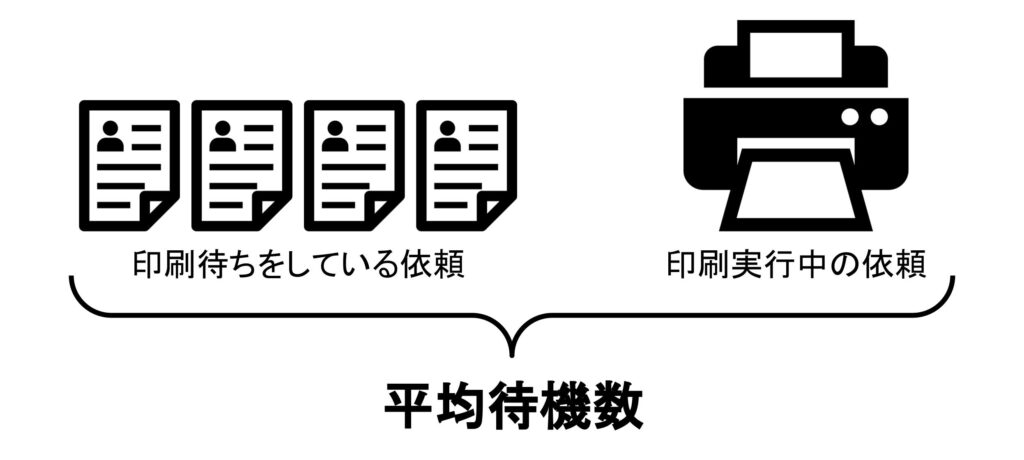
なぜ、平均待機数が平均利用率 ÷ (1-平均利用率)で表せれるのか、3つのステップで見ていきます。(ここからは少し数学っぽくなるので、苦手な人は公式だけ覚えてもらえれば大丈夫です)
Step1:平均サービス率と平均到着率のもう一つの意味
平均サービス率と平均到着率を次のように定義していました。
平均サービス率:ある時間の中で何件の依頼を実行できるのか
平均到着率 :ある時間の中で何件の依頼が来るのか
平均サービス率が高いシステムと低いシステムがあり、現在処理を実行している最中だとします。次の一瞬の間に処理が完了する確率が高いシステムはどちらでしょうか?当然、平均サービス率が高いシステムになります。
では、平均到着率が高いシステムと低いシステムがあり、次の一瞬の間にまた1つ依頼が到着する確率が高いシステムはどちらでしょうか?当然、平均到着率が高いシステムになります。
つまり、平均サービス率が高いということは、一瞬後に処理が完了している確率が高く、平均到着率が高いということは、一瞬後に1つ依頼が到着する確率が高いということです。
平均サービス率と一瞬後に処理が完了している確率、
平均到着率と一瞬後に1つ依頼が到着する確率は相関関係にある。
平均サービス率をλ、平均到着率をνと書きます。また、今を時刻tとして、それから少し時間が経過した時刻をt+Δtとします。Δtは少し経過した時間という意味です。
- 平均サービス率が高いほど、一瞬後に処理が完了している確率が高い
- Δtが大きい、つまり、経過した時間が長いほど、処理が完了している確率が高い
以上2点から、一瞬後に処理が完了している確率はλ×Δtと表すことが出来ます。
また同様に、一瞬後に1つ依頼が到着する確率はν×Δtとなります。
Step2:一瞬後に待機数がn件になっている確率
では、平均待機数を求める前に、一瞬後に待機数がn件になっている確率を求めてみます。
ここで、時刻tでの待機数がn件になっている確率をPn(t)と表すこととします。
12時に待機数が4件である確率はP4(12時)みたいな感じです。
急にPとかnとか出てきて吐き気がすると思うので、具体例を交えて丁寧に解説します。
①時刻tから一瞬後に待機数が0件になっている確率
一瞬後に待機数が0件になっているということは、次のどれかが言えます。
- 時刻tで待機数が0件で、一瞬後にも依頼が到着しない。
- 時刻tで待機数が1件で、一瞬後に処理が完了して、追加の依頼が到着しない。
これを式で表すとこのようになります。
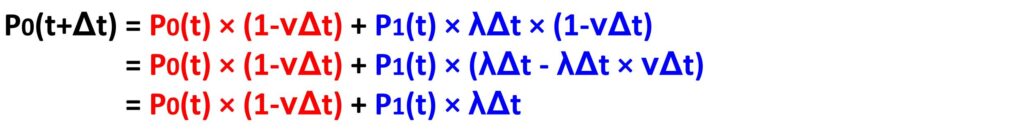
赤字の部分が「時刻tで待機数が0件で、一瞬後にも依頼が到着しない」ことを表します。
時刻tで待機数が0件である確率はP0(t)、次の瞬間に処理が到着する確率がνΔtだったので、処理が到着しない確率は(1-νΔt)になります。
青字の部分が「時刻tで処理中の依頼が1件あり、一瞬後に処理が完了して、追加の依頼が到着しない」ことを表します。
時刻tで待機数が1件である確率はP1(t)、次の瞬間に処理が完了する確率がλΔt、処理が到着しない確率は(1-νΔt)になります。λΔt×νΔtが途中で消えていますが、これは一瞬を表すΔtを2回掛けると無視していいレベルで果たしなく小さい値になるからです。
②時刻tから一瞬後に待機数が1件になっている確率
一瞬後に待機数が1件になっているということは、次のどれかが言えます。
- 時刻tで待機数が0件で、一瞬後に依頼が到着する。
- 時刻tで待機数が1件で、一瞬後に処理が完了して、追加の依頼も到着する。
- 時刻tで待機数が1件で、一瞬後に処理が完了せず、追加の依頼が到着しない。
- 時刻tで待機数が2件で、一瞬後に処理が完了して、追加の依頼が到着しない。
これを式で表すとこのようになります。
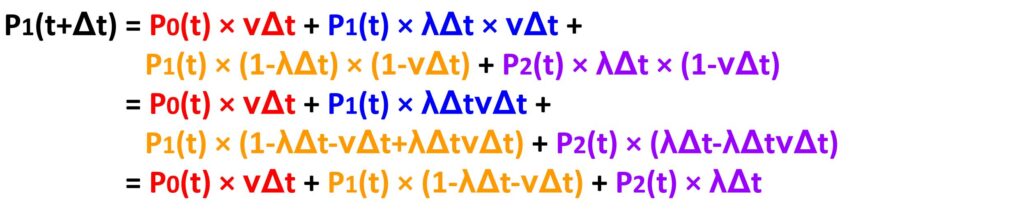
先程と同じように、λΔt×νΔtは途中で消しています。
③時刻tから一瞬後に待機数が2件になっている確率
一瞬後に待機数が2件になっているということは、次のどれかが言えます。
- 時刻tで待機数が1件で、一瞬後に処理が完了せず、追加の依頼が到着する。
- 時刻tで待機数が2件で、一瞬後に処理が完了して、追加の依頼も到着する。
- 時刻tで待機数が2件で、一瞬後に処理が完了せず、追加の依頼が到着しない。
- 時刻tで待機数が3件で、一瞬後に処理が完了して、追加の依頼が到着しない。
これを式で表すとこのようになります。
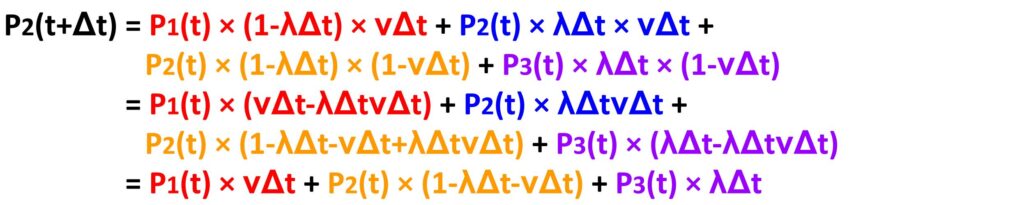
④時刻tから一瞬後に待機数がn件になっている確率
ここで、P1(t+Δt)とP2(t+Δt)の最終的に出て来た式を見比べて下さい。全く同じですよね。つまり、一瞬後に待機数がnになる確率Pn(t+Δt)は次のように考えることが出来ます。
(ただし、n=0以外の時に限ります。)
- 時刻tで待機数がn-1件で、一瞬後に処理が完了せず、追加の依頼が到着する。
- 時刻tで待機数がn件で、一瞬後に処理が完了して、追加の依頼も到着する。
- 時刻tで待機数がn件で、一瞬後に処理が完了せず、追加の依頼が到着しない。
- 時刻tで待機数がn+1件で、一瞬後に処理が完了して、追加の依頼が到着しない。
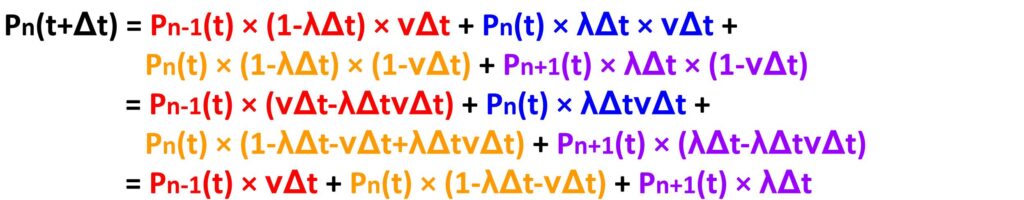
やっと、一瞬後に待機数がn件になっている確率を求めることが出来ました。
Step3:行列が安定している時を考える
Step2で次の2つの式を得ることが出来ました。
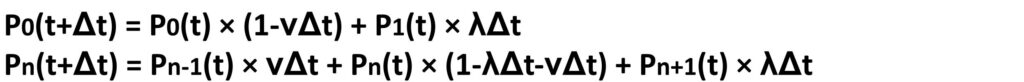
この2つの式を少しだけ変形してみましょう。
今の確率と一瞬後の確率の差
まずはP0(t+Δt)の式を変形します。変形すると言っても両辺をΔtで割っているだけです。
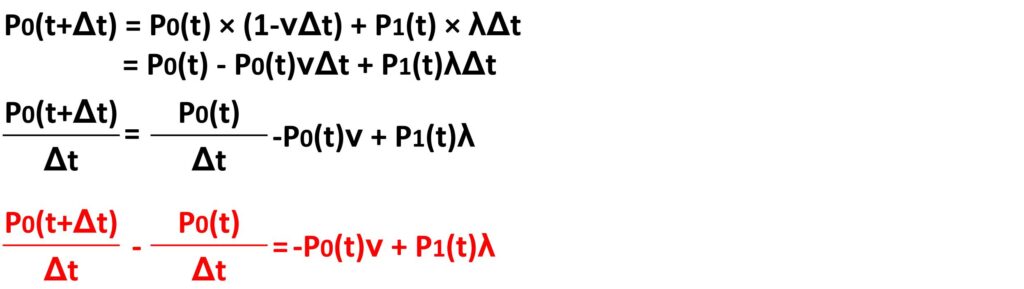
次はPn(t+Δt)の式を変形します。こちらも同じように変形すると次のようになります。

Pn(t)の確率を平均利用率とP0(t)で表す
最終的に求めたいのは、平均待機数でした。平均を求めたいので、到着する依頼の数が安定しており、依頼の列の長さが一瞬では変化しないと仮定したいと思います。
一瞬では待機数に変化がないと仮定するので、次のことが言えます。
- P0(t+Δt)-P0(t)=0
- Pn(t+Δt)-Pn(t)=0
と言うことは、上の赤字の式は次のようになりますよね。
0=-P0(t)ν + P1(t)λ
0=Pn-1(t)ν-Pn(t)(λ+ν)+Pn+1(t)λ
また、この式の両辺をλで割ってみると次のようになります。
だいぶ上の方でやった、平均利用率(ρ) = 平均到着率(ν) ÷ 平均サービス率(λ)の式があるからです。
P1(t)=P0(t)ρ
Pn+1(t)=Pn(t)(1+ρ)-Pn-1(t)ρ
この式から、P2(t)の確率を求めてみましょう。
P2(t) = P1(t)(1+ρ) – P0(t)ρとなります。下の式にn=1を代入しただけですね。
ここに、P1(t) = P0(t)ρを代入すると、
P2(t)=P0(t)ρ(1+ρ)-P0(t)ρ
→P2(t)=P0(t)ρ²
となりました。次はP3(t)の確率を求めてみましょう。
P3(t)=P2(t)(1+ρ)-P1(t)ρ
→P3(t)=P0(t)ρ²(1+ρ)-P0(t)
→P3(t)=P0(t)ρ³
以上のことから、次のことが言えます。
Pn(t)=P0(t)ρⁿ 式A
P0(t)をρで表す
では、次はPn(t)を無限に足していったらどうなるか確かめてみます。
サイコロで1、2、3、4、5、6の目が出る確率を全て足すと1になるように
時刻tで待機数が0の確率、1の確率、2の確率・・・を無限に全て足すと1になります。
P0(t)+P1(t)+P2(t)+P3(t)+・・・=1
→P0(t)+P0(t)ρ+P0(t)ρ²+P0(t)ρ³+・・・=1 式①
次に、式①の両辺にρを掛けてみます。
P0(t)ρ+P0(t)ρ²+P0(t)ρ³+P0(t)ρ⁴+・・・=ρ 式②
式①と式②を比較してみます。
P0(t)+P0(t)ρ+P0(t)ρ²+P0(t)ρ³+P0(t)ρ⁴+・・・=1
P0(t)+P0(t)ρ+P0(t)ρ²+P0(t)ρ³+P0(t)ρ⁴+・・・=ρ
最初のP0(t)以外は全て同じですよね。なので、上の式から下の式を引くとP0(t)が出ます。
P0(t)=1-ρ 式B
式Aと式Bから次のことが分かります。
Pn(t)=(1-ρ)ρⁿ
待機数の期待値を求める
待機数の期待値をLとします。Lは次の式で表せます。
L=0×P0(t)+1×P1(t)+2×P2(t)+3×P3(t)+・・・
→L=0×(1-ρ)+1×(1-ρ)ρ+2×(1-ρ)ρ²+3×(1-ρ)ρ³+・・・
→L=(1-ρ)ρ+2(1-ρ)ρ²+3(1-ρ)ρ³+・・・
→L=(1-ρ)(ρ+2ρ²+3ρ³+・・・)
→L=(ρ+2ρ²+3ρ³+・・・)-(ρ²+2ρ³+3ρ⁴・・・)
→L=ρ+ρ²+ρ³+・・・ 式③
式③の両辺にρを掛けたものと式③を比較してみましょう。
ρL=ρ+ρ²+ρ³+・・・ρ⁴ 式③
ρL=ρ+ρ²+ρ³+ρ⁴・・・ 式③にρを掛けた式
式③から式③にρを掛けた式を引いてみましょう。
(1-ρ)L=ρ
→L=ρ/1-ρ
確率の期待値はそのまま平均値だと言えるので、平均待機数は次の式で表せます。
平均待機数=ρ/1-ρ
これでやっと平均待機数を求めることが出来ました。
平均待ち時間
最後に平均待ち時間を求めてみましょう。平均待ち時間は次の式で表せます。
平均サービス時間は1回の処理に必要な時間です。
平均待ち時間=平均待機数×平均サービス時間
平均待ち時間=(平均利用率/1-平均利用率)×平均サービス時間
応用情報技術者試験での出題
応用情報技術者試験を突破するのに必要な知識はこれだけです。

出題例
応用情報技術者 午前試験
令和4年度春期問3
M/M/1の待ち行列モデルにおいて、窓口の利用率が25%から40%に増えると、平均待ち時間は何倍になるか。
ア 1.25
イ 1.60
ウ 2.00
エ 3.00
正解は”ウ”
平均待ち時間は次の式で表せます。
平均待ち時間=(平均利用率/1-平均利用率)×平均サービス時間
利用率が25%のとき
平均待ち時間=\(\displaystyle \frac{0.25}{1-0.25}\)×平均サービス時間=\(\displaystyle \frac{1}{3}\)×平均サービス時間
利用率が40%のとき
平均待ち時間=\(\displaystyle \frac{0.4}{1-0.4}\)×平均サービス時間=\(\displaystyle \frac{2}{3}\)×平均サービス時間
よって答えは2倍となります。
応用情報技術者 午前試験
令和3年度秋期問2
ATM(現金自動預払機)が1台ずつ設置してある二つの支店を統合し、統合後の支店にはATMを1台設置する。統合後のATMの平均待ち時間を求める式はどれか。ここで、待ち時間はM/M/1の待ち行列モデルに従い、平均待ち時間にはサービス時間を含まず、ATMを1台に統合しても十分に処理できるものとする。
〔条件〕
(1):平均サービス時間:Ts
(2):統合前のシステムの利用率:両支店ともρ
(3):統合後の利用者数は、統合前の両支店の利用者数の合計
ア (\displaystyle \frac{ρ}{1-ρ}\)×Ts
イ (\displaystyle \frac{ρ}{1-2ρ}\)×Ts
ウ (\displaystyle \frac{2ρ}{1-ρ}\)×Ts
エ (\displaystyle \frac{2ρ}{1-2ρ}\)×Ts
正解は”エ”
平均待ち時間と平均利用率は次の式で表せます。
- 平均待ち時間=(平均利用率/1-平均利用率)×平均サービス時間
- 平均利用率 =平均到着率/平均サービス率
平均到着率は「一定時間内に何件依頼が来るのか」で、
平均サービス率は「一定時間内に何件処理出来るか」を表す指標でした。
支店の統合後、平均到着率は2倍になりますが、平均サービス率は変わりません。
よって、平均利用率は統合前の2倍の2ρになります。
なので、平均待ち時間は(\displaystyle \frac{2ρ}{1-2ρ}\)×Tsとなります。




