基本情報の勉強を進める上で、こんな悩みを抱いたことはありませんか？
- 2の補数ってそもそもなに？
- 負数を2の補数で表現するとどうなるの？
この記事では、ITの知識が無い人でも、
2の補数がなにか分かる！
補数がどう使われるかが分かる！
負数を2の補数で表現する、というのが意味か分かる！
ようになり、基本情報の2の補数の問題なら解ける！が出来るようにします！
まずは10進数で補数について考える
補数とは、「元の数」に足し合わせることで桁上がりする最小の数のことです。例えば、10進数の「23」の補数は「77」になります。なぜなら、23+77=100となり、「77」が「23」と足し合わせて桁上がりする最小の数だからです。
補数を使うと足し算で引き算が出来る
なぜ補数なんて求める必要があるのでしょうか？
それは、補数を使えば足し算で引き算ができるからです。
意味が分かりませんね。どういうことか見ていきましょう。
「321-44=277」という計算を例に考えてみます。
補数を使う計算では、計算に使われる数字の中で最大の桁数の数字より更に1つ上の桁数の数字のうち、最小の数字をベースの数字とします。今回の例では「1000」がベースの数字になります。
次に今回の計算で引く数として使われている「44」に対して、ベースの数字「1000」を基準に補数を考えます。これは「956」ですね。なぜなら1000-44=956だからです。
では、補数を使って上の計算式を足し算で表現してみましょう。
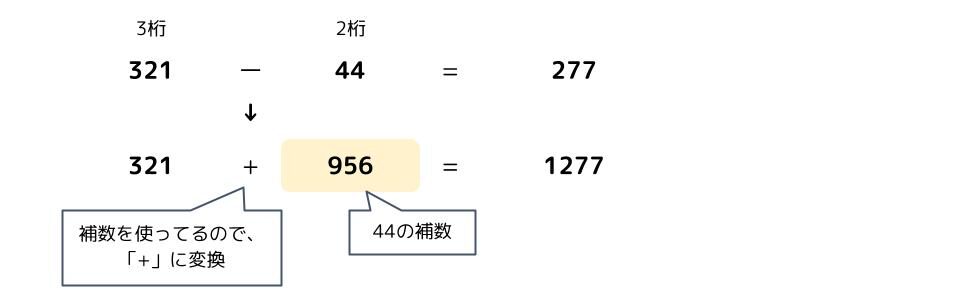
補数を使った計算では答えが「1277」になりました。
ここから最上位の1を省くと「277」となり元の計算式と同じ答えになります。
元の計算式は引き算でしたが、引き算をすることなく、足し算で答えが導けました。
つまり、補数を使いこなせば、加算器だけで引き算も出来るようになるんです！
これが補数を勉強する意味なんですね。
補数には2種類ある
補数には「基数の補数」と「減基数の補数」があります。
上で説明した補数は「基数の補数」と呼ばれるものです。
「減基数の補数」は基本情報で出題されないのでここでは説明を省略します。
「基数の補数」は「10の補数」とも呼ばれます。
2進数の補数はどうなる？
2進数の補数にも基数の補数と減基数の補数がありますが、ここでも基本情報で出題される基数の補数のみ考えていきます。ちなみに、2進数の基数の補数は2の補数と呼ばれます。
2の補数も10進数の場合と同じく、「元の数」に足し合わせることで桁上がりする最小の数のことです。例えば「101」の補数は「011」になります。なぜなら101+011=1000だからです。
2の補数の求め方には公式があります。
- 元の数の0と1を反転させる
- 反転させた数に1を足す
「101」の0と1を反転させると「010」になり、これに1を足すと「011」になります。
なので「011」は「101」の2の補数です。
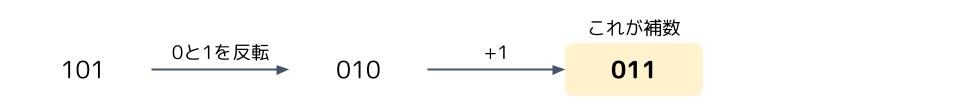
負数を2の補数で表す
コンピュータは0と1だけで全ての情報を制御します。
なので、負の数(負数)も0と1で制御しないといけません。
「-1001」なんて数字は扱えないんですね。
じゃあ、どうすれば負数を表現できるでしょうか？
最上位が0の場合は正数、1の場合は負数とすれば良いんですね。
これが「負数を2の補数で表す」ということです。
では、負数「11011110」は10進数で言うと何になるのでしょうか？
ここで出てくるのが補数です。「11011110」は「00100010」の2の補数です。「00100010」=「34」なので、「11011110」=「-34」となります。
本当に「11011110」=「-34」で良いのか、「64-34=30」を例に検証します。
この計算式を、負数を2の補数で表現する2進表記法で表すと、こうなります。
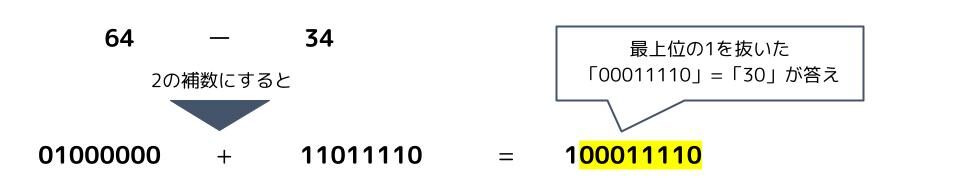
「64」は「01000000」、「-34」は「11011110」で
この2つを足すと「100011110」になり、最上位の1を抜いた「00011110」が答えになります。「00011110」は「30」なので、ちゃんと計算できていることが分かりますね。
基本情報、出るところだけまとめ！
2の補数を求めたければ、0と1を反転して、+1をする。
負数を2の補数で表現するとき、最上位が0なら正数、1なら負数になる。
基本情報技術者試験での出題例
サンプル問題問1
基本情報技術者
科目A サンプル問題問1
負数を2の補数で表すとき，8ビットの2進正数nに対し－nを求める式はどれか。ここで，＋は加算を表し，ORはビットごとの論理和，XORはビットごとの排他的論理和を表す。
ア (n OR 10000000)＋00000001
イ (n OR 11111110)＋11111111
ウ (n XOR 10000000)＋11111111
エ (n XOR 11111111)＋00000001
正解は”エ”
2の補数の求め方は
- 元の数の0と1を反転させる
- 反転させた数に1を足す
です。これに該当するのはエですね。
論理和・排他的論理和の意味が分からない人はこちらの記事をご覧ください。
平成30年度春期問1
基本情報技術者 午前試験
平成30年度春期問1
ある整数値を，負数を2の補数で表現する2進表記法で表すと最下位2ビットは”11″であった。10進表記法の下で，その整数値を4で割ったときの余りに関する記述として，適切なものはどれか。ここで，除算の商は，絶対値の小数点以下を切り捨てるものとする。
ア その整数値が正ならば3
イ その整数値が負ならば－3
ウ その整数値が負ならば3
エ その整数値の正負にかかわらず0
正解は”ア”
4桁の2進数を例にしてこの問題を考えてみましょう。
負数を2の補数で表現するので、0000~0111が正の数、1000~1111が負の数となります。
●ある整数値が正の場合
最下位2ビットが’11’なので、例えば’0011’や’0111’が当てはまりますね。’0011’は10進数で’3’、’0111’は10進数で’7’になり、それぞれを4で割ると余りは3になります。
●ある整数値が負の場合
最下位2ビットが’11’なので、例えば’1011’や’1111’が当てはまります。’1011’は’0101’の2の補数で、’1111’は’0001’の2の補数です。’0101’は10進数で’5’を、’0001’は10進数で’1’を表すので、’1011’は’-5’を、’1111’は’-1’を表します。
-5÷4=-1.25ですが、「商は絶対値の小数点以下を切り捨てる」と書いてあるので、商は-1となり、-5÷4=-1余り-1と表せます。同様にすると-1÷4=0余り-1となるので、ある整数値が負の場合は余りが-1になることが分かります。
以上のことから、
・整数値が正の場合、余りは3
・整数値が負の場合、余りは-1
となるので、答えはアです。
