基本情報の勉強を進める上で、こんな悩みを抱いたことはありませんか？
- そもそも2進数ってなんだっけ？
- 2進数を10進数に変換する方法が分からない
- 10進数を2進数に変換する方法が分からない
この記事では、ITの知識が無い人でも、
2進数がなにか分かる！
2進数と10進数を変換できる！
ようになり、基本情報の2進数の問題なら解ける！が出来るようにします！
2進数は0と1だけで数を数える方法
2進数とは「0」と「1」だけで数を表す方法です。
私たちが普段使う10進数では、0から9までの10個の数字で数を表します。
10進数では、「9」より1つ大きい数字は「10」になります。これは「9」より大きい1桁の数字が無いからですね。
同じように、2進数では「1」より1つ大きい数字は「10」になります。2進数で最も大きい1桁の数字は「1」だからです。
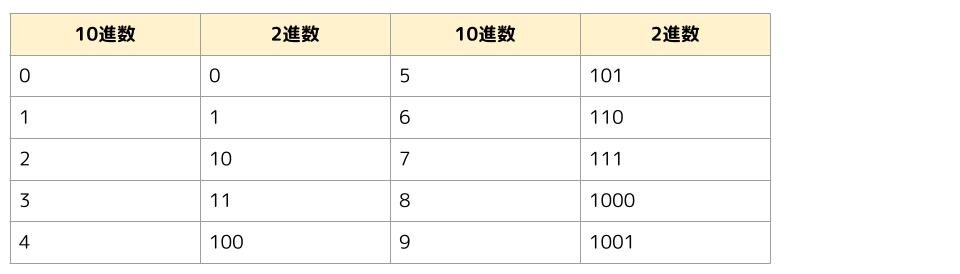
なぜコンピュータの勉強で2進数を学ぶのか
コンピュータは電子機器です。なので、電気を使って様々な処理をしています。
電気にはオンとオフの2つの状態しかありません。この2つの状態を「1」と「0」で表現するのが便利なので、「1」と「0」で数を表す2進数がコンピュータでは使われるという訳です。
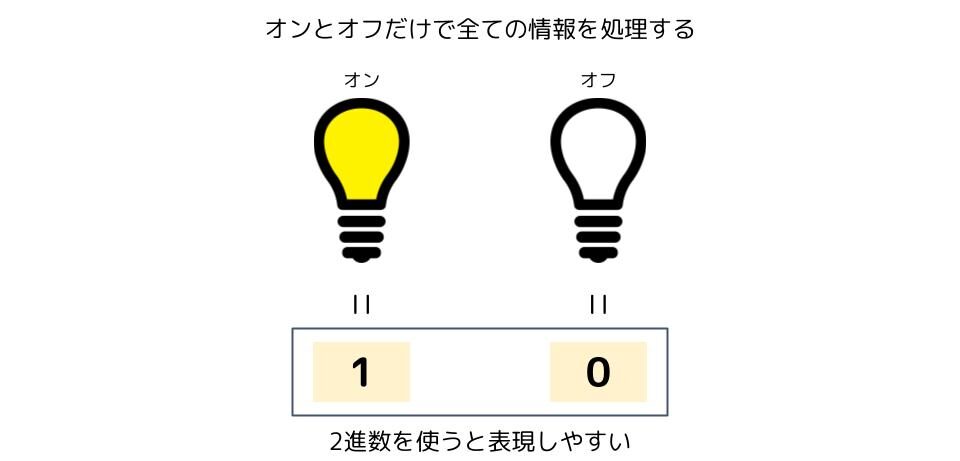
2進数を10進数に変換する方法
2進数を10進数に変換する方法を学ぶ前提として、位取り記数法の考え方を知って欲しいと思います。難しい名前ですが、実は私たちは普段、位取り記数法で数を表現しています。
例えば、10進数で「2356」と記載があれば、1000が2つ、100が3つ、10が5つ、1が6つあることを表しています。位は10倍ずつ上がっていくので、右から4つ目の位は1000の位で、そこにある「2」は「2000」を意味すると無意識で理解しています。この考え方が位取り記数法です。
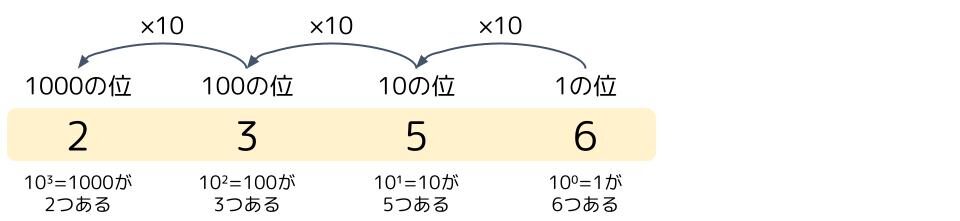
では、2進数の場合はどうなるでしょうか？
2進数の場合も同じように考えます。「1011」と記載があれば、8が1つ、4が0つ、2が1つ、1が1つあることを表しています。2進数の場合、位は2倍ずつ上がっていくので、右から4つ目の位は8の位で、そこにある「1」は「8×1=8」を意味します。同じように全ての桁の値を考えていくと、2進数の「1011」は10進数の「11」だと計算出来ます。これが2進数を10進数に変換する方法です。
10進数を2進数に変換する方法
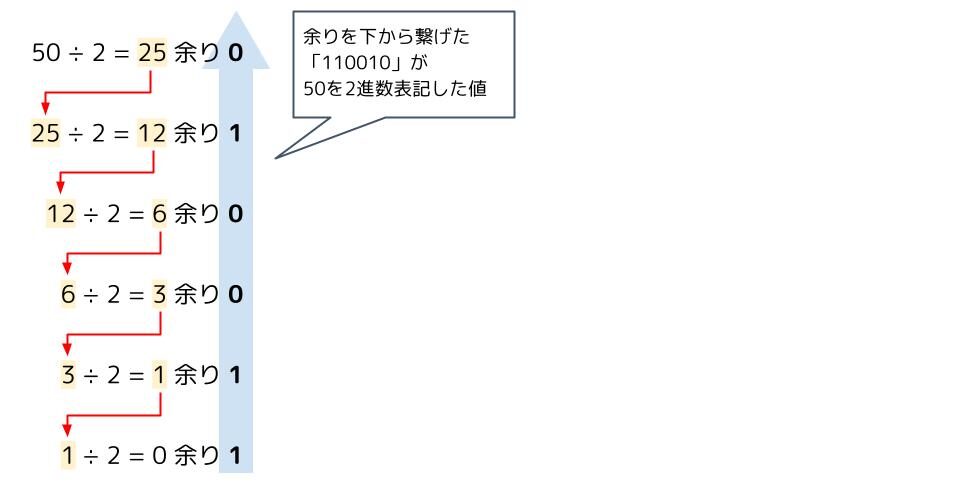
10進数を2進数に変換するには、ひたすら2で割って余りを繋げます。
「50」を2進数に変換してみましょう。
- 「50」を2で割る。50÷2=25余り0
- ①の商である「25」を2で割る。25÷2=12余り1
- ②の商である「12」を2で割る。12÷2=6余り0
- ③の商である「6」を2で割る。6÷2=3余り0
- ④の商である「3」を2で割る。3÷2=1余り1
- ⑤の商である「1」を2で割る。1÷2=0余り1
- 商が「0」になったので2で割るのはここで終わり。
- 余りを下から繋げると「110010」となる。
これが「50」を2進数表記した値になる。
なぜ上の方法で10進数を2進数に変換出来るのか
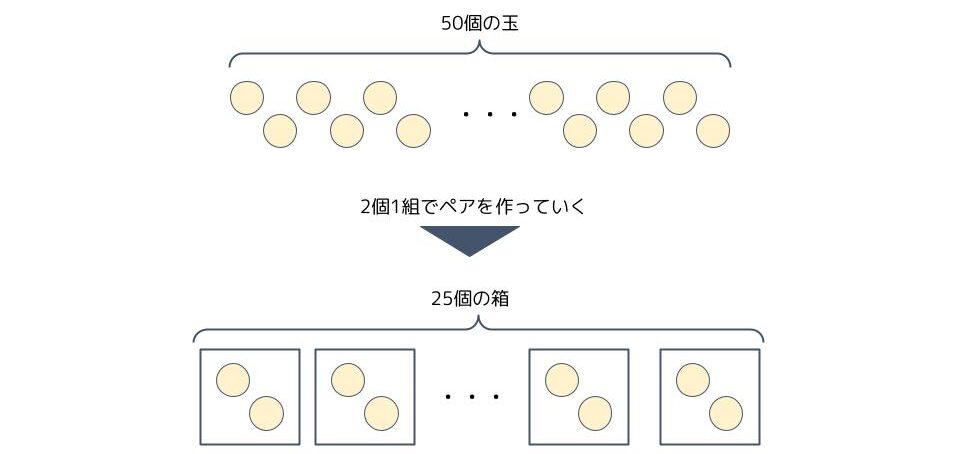
「50」を2で割り続ける操作を図にしてみましょう。
「50÷2=25余り0」は50個の玉で2個1組のペアを作るとき、25個の箱が出来て、余りの玉が無いことを意味します。
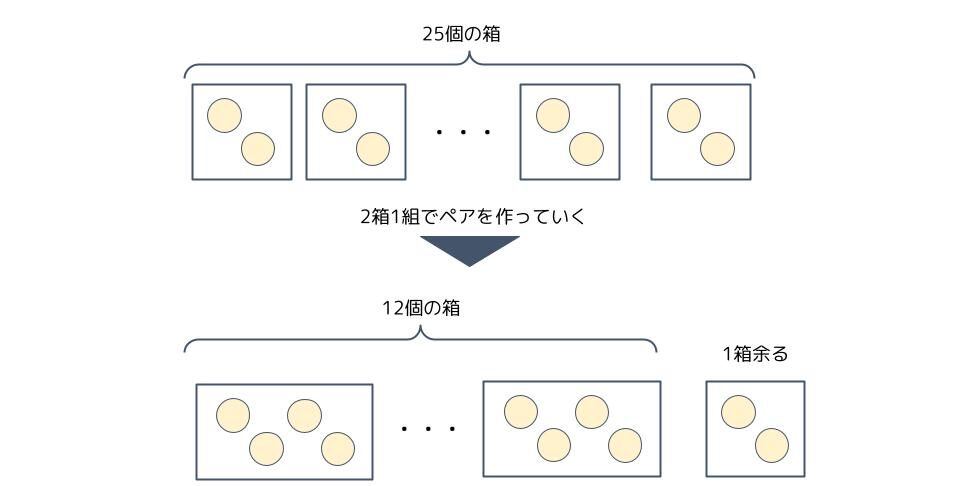
次の「25÷2=12余り1」は上で作った2個入りの箱で、更に2箱1組のペアを作るとき、12個の箱が出来て、1箱余ることを意味します。
同じように、「12÷2=6余り0」は上で作った4個入りの箱で、更に2箱1組のペアを作るとき、6個の箱が出来て、余りの箱が無いことを意味し、
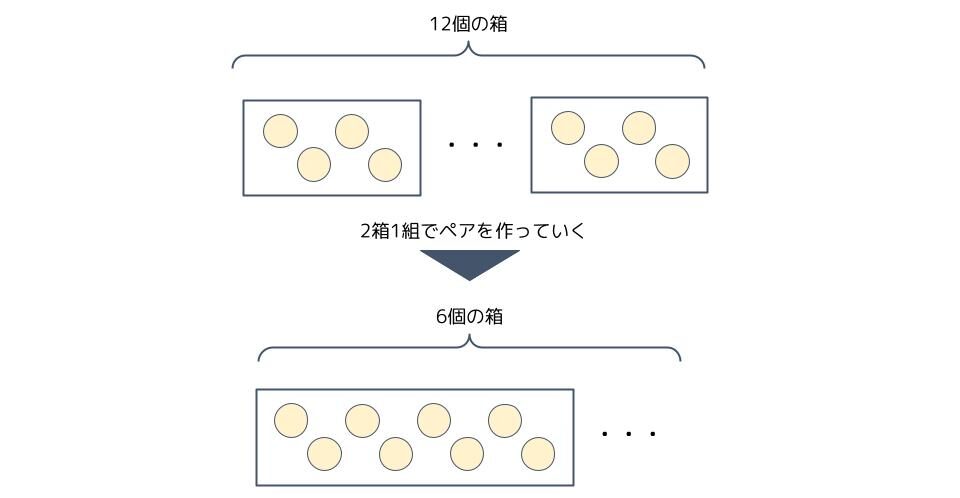
「6÷2=3余り0」は上で作った8個入りの箱で、更に2箱1組のペアを作るとき、3個の箱が出来て、余りの箱が無いことを意味し、
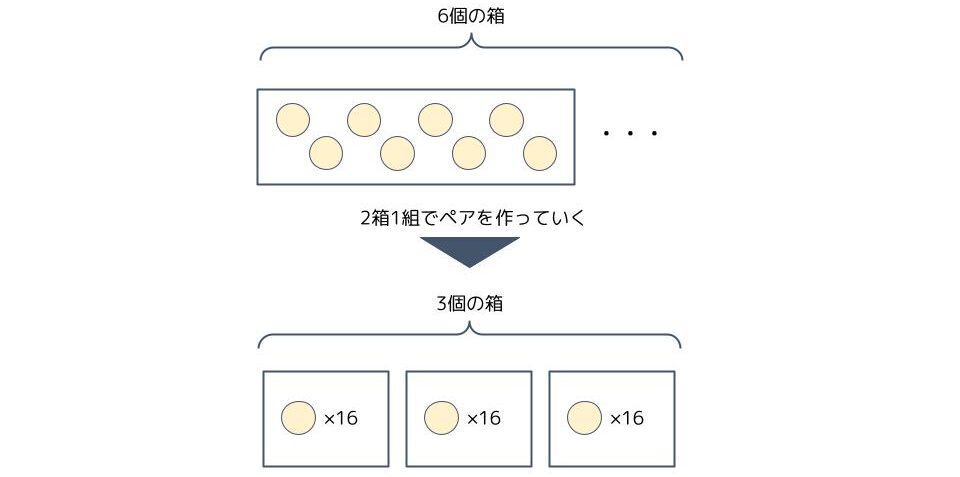
「3÷2=1余り1」は上で作った16個入りの箱で、更に2箱1組のペアを作るとき、1個の箱が出来て、1箱余ることを意味し、
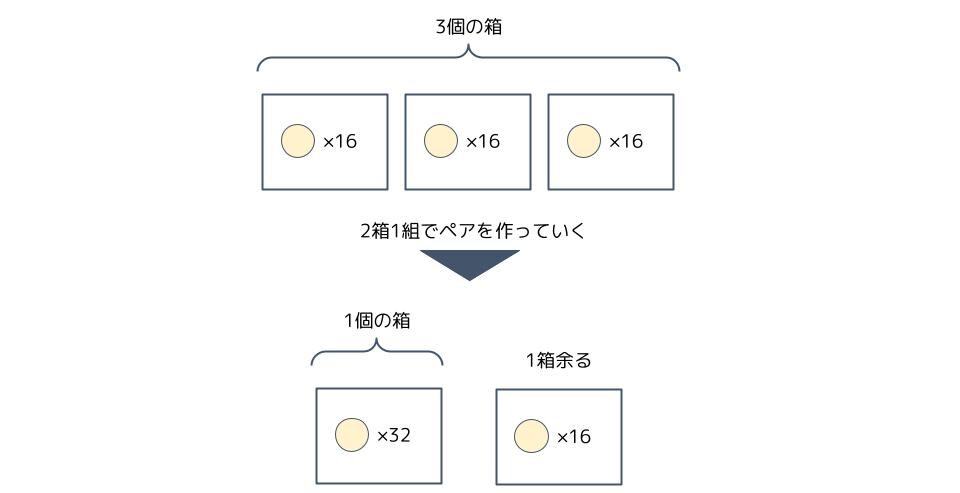
最後の「1÷2=0余り1」は上で作った32個入りの箱で、更に2箱1組のペアを作るとき、ペアは出来ずに、1箱余ることを意味します。
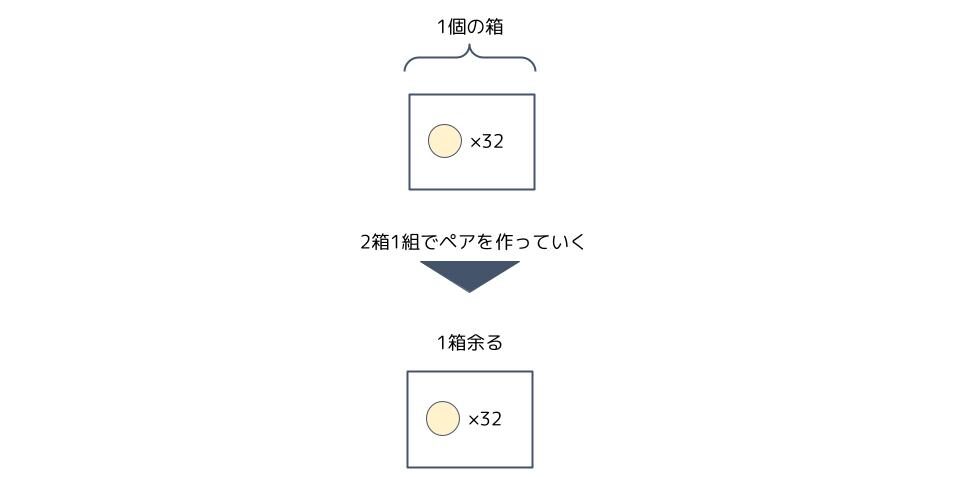
以上のことから、「50」個の玉をそれぞれの箱に振り分けていくと、
「32個入りの箱」が1箱、「16個入りの箱」が1箱、「8個入りの箱」が0箱、
「4個入りの箱」が0箱、「2個入りの箱」が1箱、玉の余りが出ないことが分かりました。
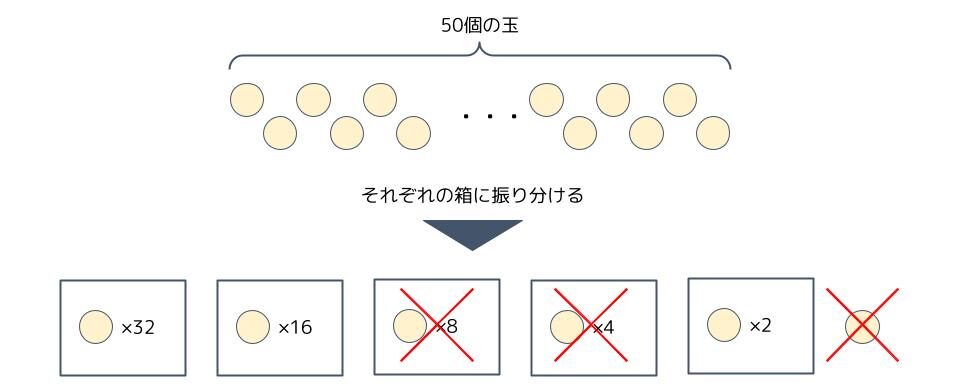
2進数の数字の各桁は、それぞれ各位の値が何個あるのかを表していました。
なので、上の箱はこう表すことも出来ますよね。
これで、「50」を2進数で表記することが出来ました。
小数・分数の10進数を2進数に変換する方法
小数・分数の10進数は次の方法で2進数に変換出来ます。
- 小数・分数の10進数が整数になるまで2で掛けます
- ①の整数を2進数に変換します
- ①で掛けた2の数だけ1を右に移動します
これが2進数に変換した値です
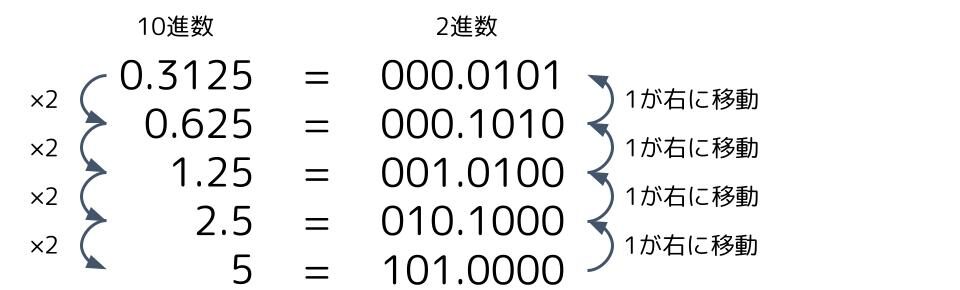
実際に0.3125を2進数に変換してみましょう。
「0.3125」を整数になるまで2で掛けると「5」になります。「5」は2進数で「101」です。「5」になるまで4回、2を掛けたので「101」の1を4回右に移動しましょう。
移動した結果出て来た「0.0101」が「0.3125」を2進数に変換した値になります。
なぜ上の方法で小数・分数の10進数を2進数に変換出来るのか
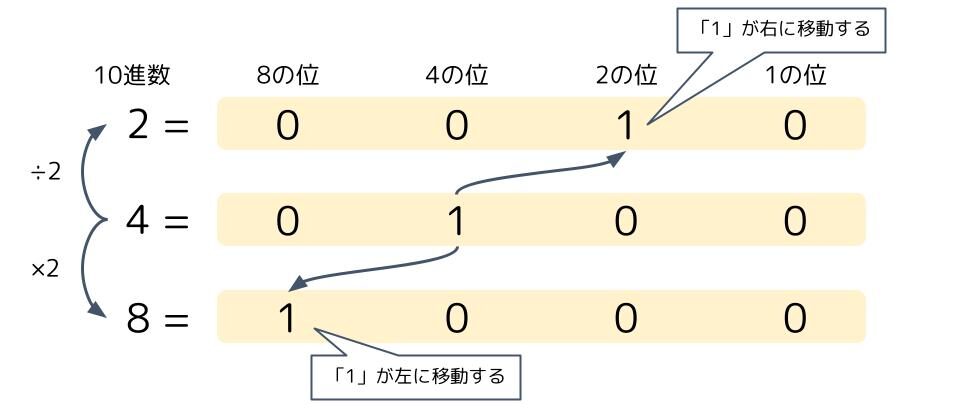
10進数の2、4、8をそれぞれ2進数に変換してみましょう。
2→4→8と、10進数の数が2倍になると、2進数の1が左に移動し、
逆に、8→4→2と、10進数の数が半分になると、2進数の1が右に移動します。
なぜなら、2進数では位の数が2倍ずつ増えていくからなんですね。
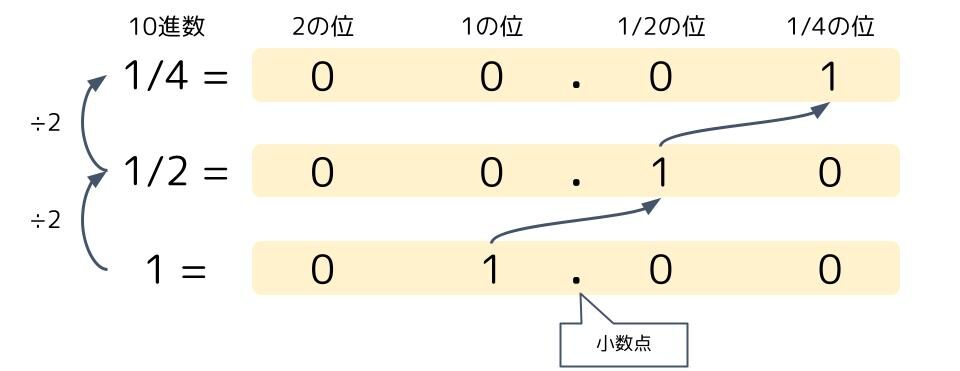
これは小数でも同じことが言えます。
10進数が半分になると、2進数の1が右に移動しますね。
では、改めて「0.3125」を2進数に変換してみましょう。
「0.3125」の2進数が何かは分からないですが、「0.3125」に2を4回掛けた「5」の2進数は「101」だと分かりますね。
では、「0.3125」の2進数は？というと、上の話から「101」の1を4回右に移動したものになります。よって、答えは「0.0101」になるんですね。
基本情報、出るところだけまとめ！
2進数にも「位」がある！「位の数×格納されている数」をして全部足すと10進数に変換できる。
10進数の数を商が0になるまで2で割り続け、余りを下から繋げたものが2進数に変換した数。
小数・分数の10進数を2進数に変換するには、10進数を整数になるまで2で掛け続けて、その整数を2進数に変換した後、2で掛けた回数分、1を右に移動する。
基本情報技術者試験での出題例
令和元年度秋期問1
基本情報技術者
午前試験 令和元年度秋期問1
次の流れ図は，10進整数 j(0＜j＜100) を8桁の2進数に変換する処理を表している。2進数は下位桁から順に，配列の要素 NISHIN(1) から NISHIN(8) に格納される。流れ図のa及びbに入る処理はどれか。ここで，j div 2 はjを2で割った商の整数部分を，j mod 2 はjを2で割った余りを表す。
正解は”エ”
10進数「5」を2進数「00000101」に変換する処理を例にア～エの検証をします。
NISHIN(1) = 1
NISHIN(2) = 0
NISHIN(3) = 1
NISHIN(4~8) = 0
になるはずです。
【アの検証】
・k=1
[a]：5 div 2 = 2 → j
[b]：2 mod 2 = 0 → NISHIN(1) この時点で違うのでアは×です
【イの検証】
・k=1
[a]：5 mod 2 = 1 → j
[b]：1 div 2 = 0 → NISHIN(1) この時点で違うのでイは×です
【ウの検証】
・k=1
[a]：5 div 2 = 2 → NISHIN(1) この時点で違うのでウは×です
[b]：5 mod 2 = 1 → j
【エの検証】
・k=1
[a]：5 mod 2 = 1 → NISHIN(1)
[b]：5 div 2 = 2 → j
・k=2
[a]：2 mod 2 = 0 → NISHIN(2)
[b]：2 div 2 = 1 → j
・k=3
[a]：1 mod 2 = 1 → NISHIN(3)
[b]：1 div 2 = 0 → j
・k=4
[a]：0 mod 2 = 0 → NISHIN(4)
[b]：0 div 2 = 0 → j
これ以降、NISHINには0が入ります。よってエが正しいことが分かります。
平成31年度春期問1
基本情報技術者
午前試験 平成31年度春期問1
10進数の演算式7÷32の結果を2進数で表したものはどれか。
ア 0.001011
ウ 0.00111
イ 0.001101
エ 0.0111
正解は”ウ”
\(\frac{7}{32}\)を2進数に変換した結果が答えになります。
分数の10進数を2進数に変換する方法はこの通りです。
- 小数・分数の10進数が整数になるまで2で掛けます
- ①の整数を2進数に変換します
- ①で掛けた2の数だけ1を右に移動します
これが2進数に変換した値です
まずは\(\frac{7}{32}\)が整数「7」になるまで5回、2で掛けます。
10進数の「7」は2進数で「111」なので、「111」の1を5回右に移動します。これで出た「0.00111」が答えになります。
平成29年度秋期問1
基本情報技術者
午前試験 平成29年度秋期問1
数値を2進数で表すレジスタがある。このレジスタに格納されている正の整数xを10倍する操作はどれか。ここで，桁あふれは，起こらないものとする。
ア xを2ビット左にシフトした値にxを加算し，更に1ビット左にシフトする。
イ xを2ビット左にシフトした値にxを加算し，更に2ビット左にシフトする。
ウ xを3ビット左にシフトした値と，xを2ビット左にシフトした値を加算する。
エ xを3ビット左にシフトした値にxを加算し，更に1ビット左にシフトする。
正解は”ア”
ここではx=5を10倍にする操作を例に答えを考えてみましょう。
10進数の「5」は2進数で「101」、10進数の「50」は2進数で「110010」です。
【アの検証】
xを2ビット左にシフトした値=10100
これにxを加算した値=10100+101=11001
更に1ビット左にシフトした値=110010
よってアは正しいことが分かります。
【イの検証】
xを2ビット左にシフトした値=10100
これにxを加算した値=10100+101=11001
更に1ビット左にシフトした値=1100100
よってイは間違いです。
【ウの検証】
xを3ビット左にシフトした値=101000
xを2ビット左にシフトした値=10100
これらを加算した値=111100
よってウは間違いです。
【エの検証】
xを3ビット左にシフトした値=101000
これにxを加算した値=101000+101=101101
更に1ビット左にシフトした値=1011010
よってエは間違いです。
