2進数と10進数を変換する方法を解説｜絶対分かるちゃちゃちゃITブログ

この記事では2進数を10進数に変換する方法と10進数を2進数に変換する方法と
小数・分数で表現された10進数を2進数に変換する方法についてIT初心者にも分かりやすく解説します。

2進数を10進数に変換する方法

数字の各桁には重みがある。例えば、2進数の1桁目には「1」の重み、2桁目には「2」の重み、3桁目には「4」の重みがある。
2進数の数字に各桁の重みを掛けた数字が10進数の数字になる。例えば、2進数の「101」は1×1+0×2+1×4=5となり、10進数に変換した数字は「5」となる。

10進数を2進数に変換する方法

10進数の数字を商(答え)が1になるまで割り続けて、割り算の余りを繋げた結果が2進数に変換した数字となる。例えば、10進数の「11」の場合、
①11÷2=5余り1
②5÷2=2余り1
③2÷2=1余り0
となり、③の商→③の余り→②の余り→①の余りを繋げた「1011」が2進数に変換した後の数字となる。

小数・分数で表現された10進数を2進数に変換する方法

小数・分数で表現された10進数を整数になるまで2で掛け続け、最後に出て来た整数を2進数に変換する。変換した2進数の小数点を2で掛けた数だけ左に移動した結果が、最初の小数・分数で表現された10進数を2進数に変換した結果。
例えば、10進数の「1.25」を2進数に変換すると、
①1.25×2=2.5、2.5×2=5となり、2を2回掛けたら整数の5になる。
②10進数の「5」を2進数に変換すると「101」になる。
③「101」の右端から小数点を2回移動した「1.01」が2進数に変換した結果となる。

基本情報では2進数を10進数に変換する問題、10進数を2進数に変換する問題が頻出します。是非最後までご覧ください。

数える時に大切な「位」
- 10進数の数え方
2進数を10進数に変換する
- 2進数を10進数に変換する方法
10進数を2進数に変換する
- 10進数を2進数に変換する方法（整数編）
  - （おまけ）なぜ上の公式は成り立つのか
- 10進数を2進数に変換する方法（小数・分数編）
  - （おまけ）なぜ上の公式は成り立つのか
基本情報技術者試験での出題例
基本情報に関するの他の記事

数える時に大切な「位」

10進数の数え方

10進数は0~9の10個の数字を使って数を数えます。10進数では0,1,2,3,4,5,6,7,8,9と10個の数字で1桁の数字を表現した後、2桁目の数を1上げて1桁目の数字を0に戻します。

つまり、2桁目の数字には10個分の数字の重みがあると言えます。もっと分かりやすく飴玉を使って考えてみましょう。例えば、「16」という数字は2桁目が1、1桁目が6です。なので下の画像のように、10個入りの袋が1つとばらの飴玉が6個あるという風に考えることが出来ます。これが、数字の「位」による重みです。

例えば、「234」という数字は3桁目が2、2桁目が3、1桁目が4です。3桁目は10個入りの袋が更に10個入った箱のようなイメージです。10個入りの袋が10個箱に入っているので、3桁目に入っている飴玉は10×10=10²=100個となります。

同じように、4桁目は10個入りの袋が10個入った箱が10個トラックに入っていると考えられるので、4桁目に入っている飴玉は10×10×10=10³=1000個となります。

10進数の位の重み
1桁目・・・10⁰=1（バラの飴玉）
2桁目・・・10¹=10（袋に入った飴玉）
3桁目・・・10²=100（箱に入った飴玉）
4桁目・・・10³=1000（トラックに入った飴玉）
n桁目・・・\( 10^{ n-1} \)

2進数を10進数に変換する

2進数は0と1の2つの数字を使って数を数えます。2進数では0,1と2個の数字で1桁の数字を表現した後、2桁目の数を1上げて1桁目の数字を0に戻します。

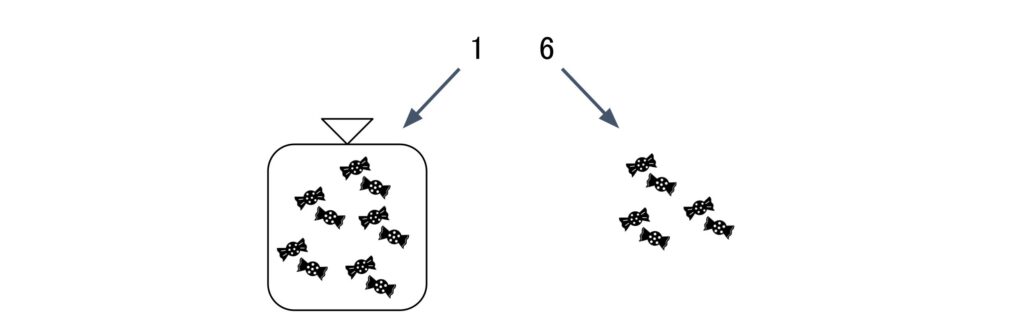
つまり、2桁目の数字には0と1の2個分の数字の重みがあると言えます。飴玉で例えると、2桁目は飴玉2個入りの袋で、1桁目は飴玉1個のバラになります。なので、例えば、2進数の「11」は飴玉3個分になるので、2進数の「11」＝10進数の「3」になります。

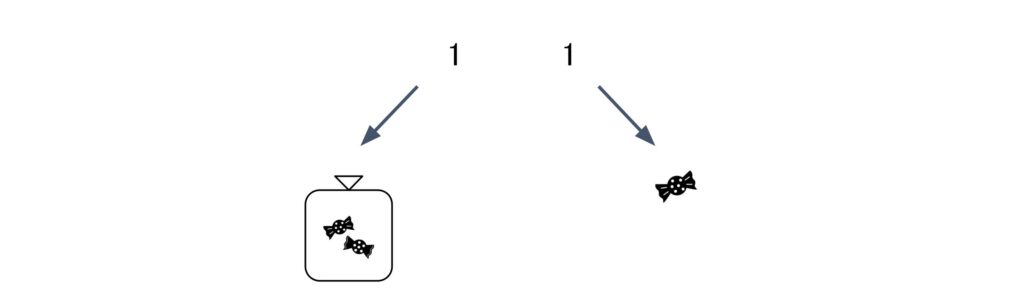
3桁目も10進数と同様に、2つ入りの袋が2つ入った箱と考えることが出来ます。2進数は使える数字が0と1の2つしか無いので、2ずつ位の重みが上がっていくのがポイントです。なので、例えば、2進数の「110」は、2²=4個の箱が1つ、2個の袋が1つなので10進数では「6」になります。

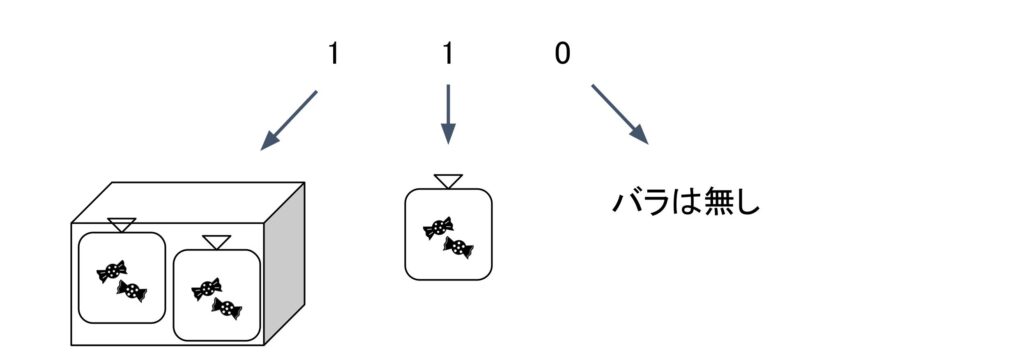
2進数の位の重み
1桁目・・・2⁰=1（バラの飴玉）
2桁目・・・2¹=2（袋に入った飴玉）
3桁目・・・2²=4（箱に入った飴玉）
4桁目・・・2³=8（トラックに入った飴玉）
n桁目・・・\( 2^{ n-1} \)

2進数を10進数に変換する方法

2進数の位にそれぞれ重みを付けていき、最後に足した数字が10進数となります。例で2進数の「110101」を10進数に変換します。「110101」にそれぞれ重みを付けて足し算をすると、32になるので、2進数の「110101」は10進数の「32」であることが分かります。

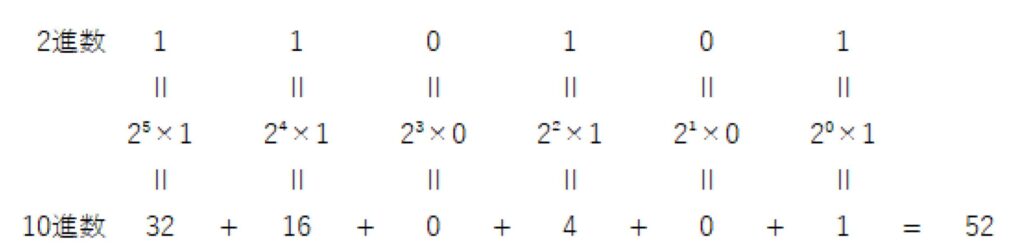
10進数を2進数に変換する

逆に10進数を2進数に変換する方法を考えてみます。先程書いたとおり、2進数の位にはそれぞれ重みがありました。位によって入れることが出来る飴玉の数が違いましたね。

10進数の「5」を2進数に変換してみましょう。5個の飴玉を梱包していきます。飴玉が8個入るトラックだと丁度入り切らないのでトラックは使えません。飴玉が4個入る箱は使えそうなので箱に梱包します。すると飴玉が1個余るのでバラの飴玉を1つ持ちます。箱は3桁目の重み、バラの飴玉は1桁目の重みだったので、10進数の「5」は2進数で「101」になることが分かります。

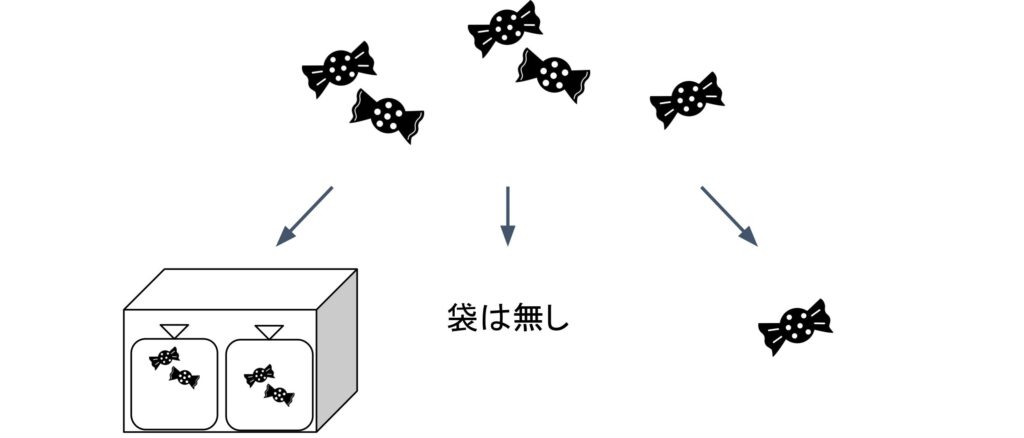
5個の飴玉を2個入る袋2つに入れることは出来ないのか？と思った人もいると思いますが、これは出来ません。2進数では0と1しか使えないので、袋を2つ作ることは出来ません。袋2つは箱1つと同じなので、箱に変換されます。

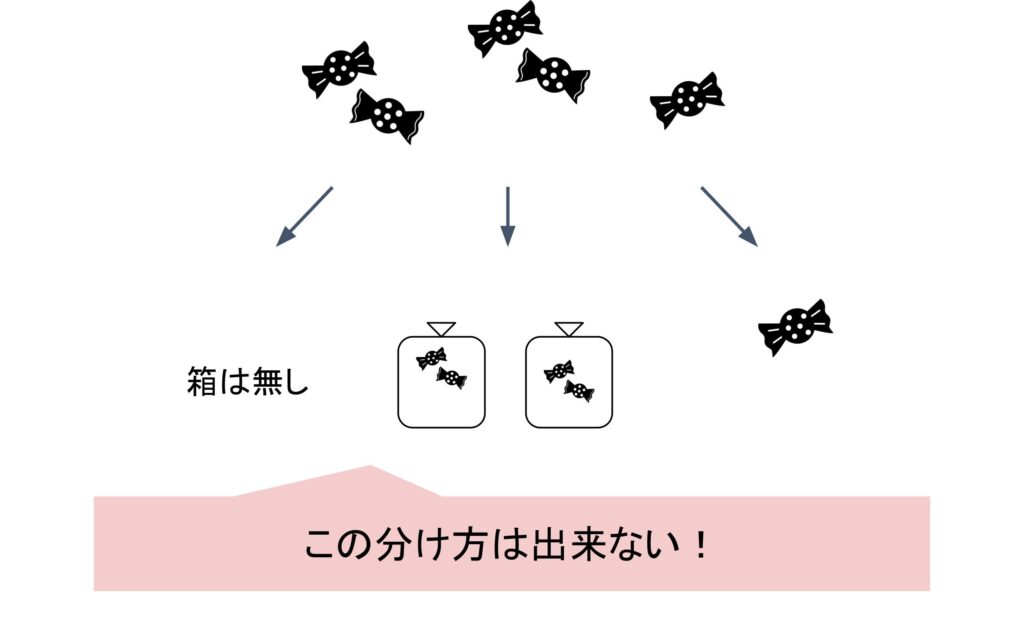
このように、10進数の数を2進数の位の重みで分散させた結果が、2進数で表記した数になります。

10進数を2進数に変換する方法（整数編）

10進数の数を商が1になるまで割り続けます
割り算の余りを繋げた結果が2進数に変換した結果です

実際に50を2進数に変換してみましょう。「50」を2で割り続けて出て来た余りを一番下から繋げ合わせると2進数に変換した結果である「110010」になります。

（おまけ）なぜ上の公式は成り立つのか

50を2進数に変換した例から公式の意味を考えてみたいと思います。

最初に50÷2=25余り0と求めました。これは、50個の飴玉を梱包していった時にバラの飴玉が1つも出てこないことを表します。2で割った余りが0ということは全て2つ入りの袋に入れることが出来るということなので、バラの飴玉は発生しませんよね。なので、「110010」の1桁目は0になっているのです。

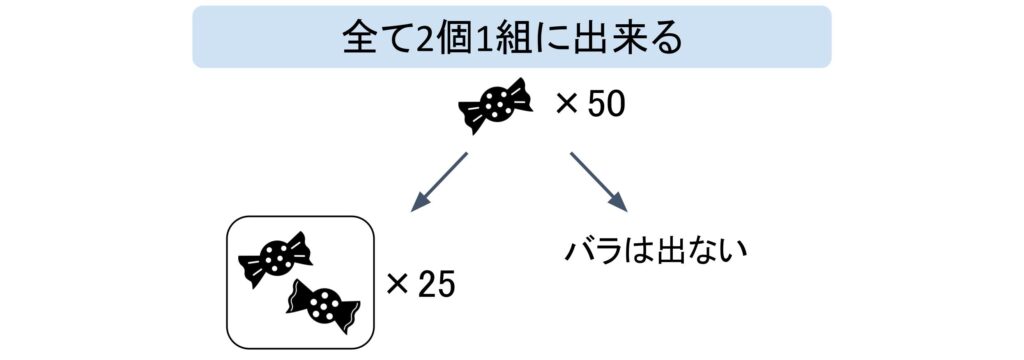
次に25÷2=12余り1と求めました。これは2個1組にした25組の飴玉を更にペアにしたときに、1組余るということを表します。なので、「110010」2¹を表す2桁目は1になります。

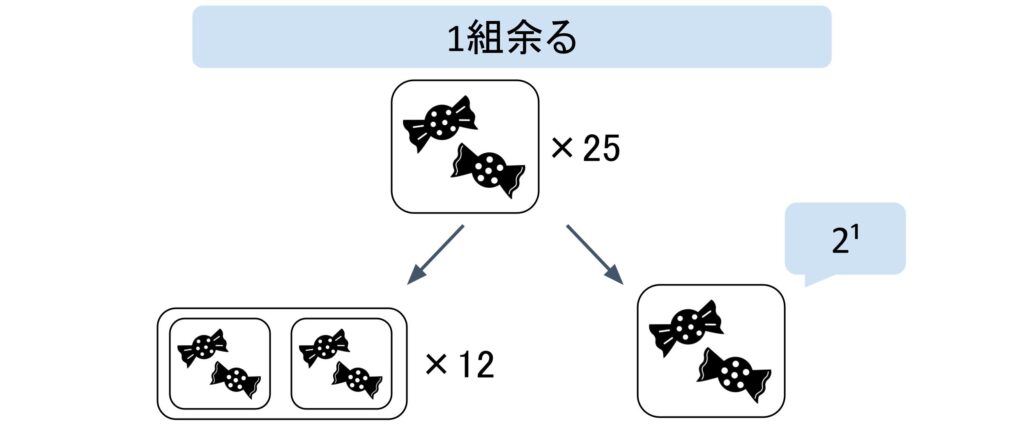
同じように、組を作り続けて行きます。

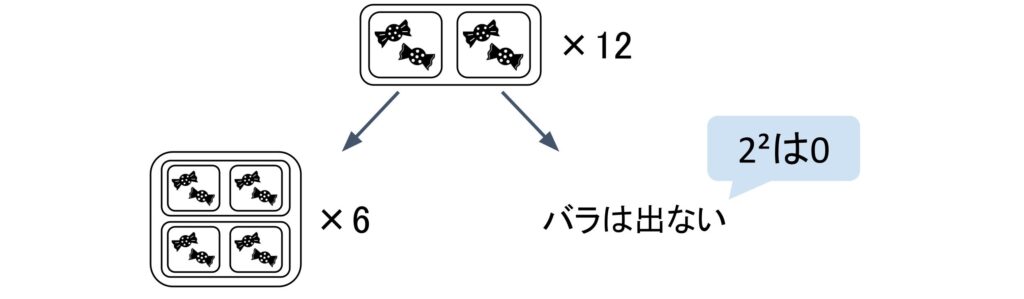
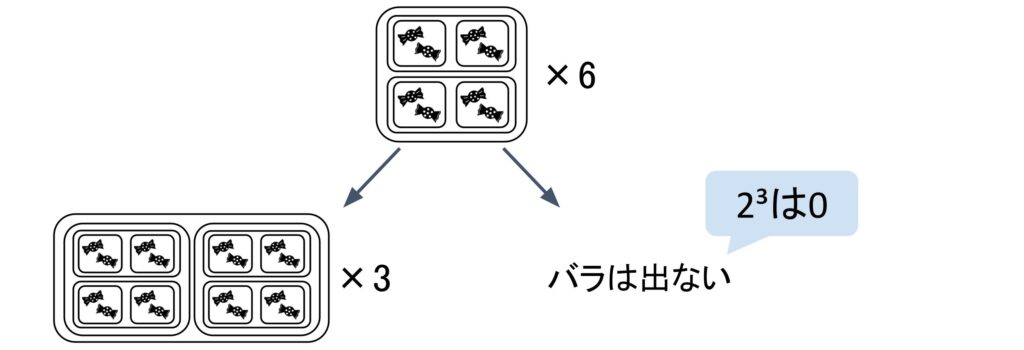
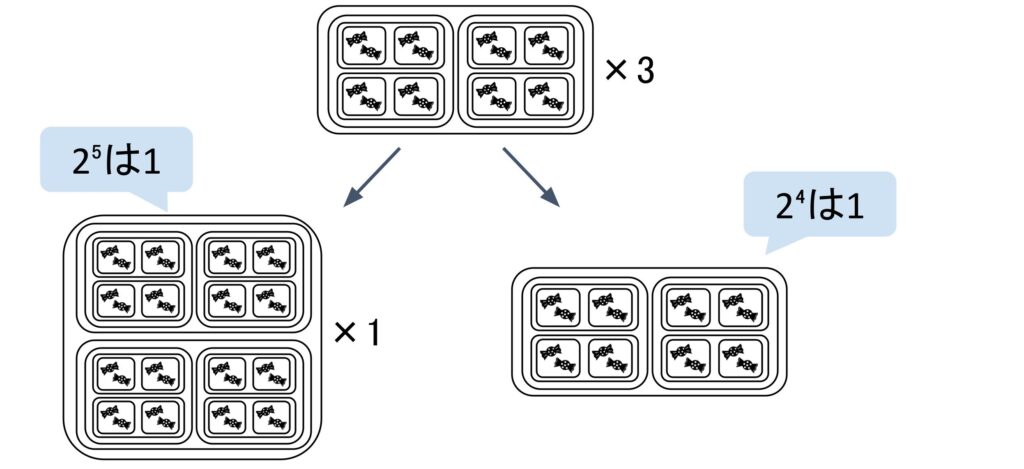
これ以上ペアが出来なくなるまで、ペアを作り続けた結果、
50=(2⁵×1)+(2⁴×1)+(2³×0)+(2²×0)+(2¹×1)+(2⁰×0)となることが分かりました。よって、50の2進数表現は「110010」になります。

10進数を2進数に変換する方法（小数・分数編）

10進数の小数・分数が整数になるまで2で掛けます
最後に出て来た整数を2進数に変換します
掛け合わせた2の数だけ右端から小数点を左に移します。
その結果が2進数に変換した結果です

それでは実際に0.3125を2進数に変換してみます。まず0.3125を整数になるまで2で掛け続けると5になります。

5は2進数で「101」です。また2で掛けた回数は4回です。なので「101」の右端から小数点を4回左に移動します。その結果出て来た「0.0101」が2進数に変換した結果です。

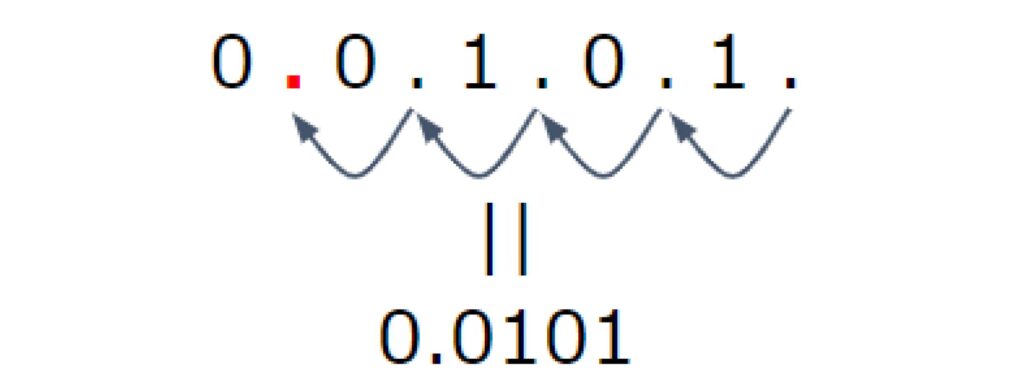
（おまけ）なぜ上の公式は成り立つのか

2進数で表現した数字にはそれぞれ2の倍数の重みがあると言いました。なので、2進数の「1」に2を掛けると「10」になりますし、2×2=4を掛けると「100」になります。また同じ考え方で「10」を2で割ると「1」になりますし、4で割ると「0.1」になります。

つまり、10進数の「5」を2×2×2×2=16で割った「0.3125」を2進数に変換した値は、2進数の「101」を16で割った「0.0101」になるという訳です。

基本情報技術者試験での出題例

令和元年度秋期問1

基本情報技術者
午前試験　令和元年度秋期問1

次の流れ図は，10進整数 j(0＜j＜100) を8桁の2進数に変換する処理を表している。2進数は下位桁から順に，配列の要素 NISHIN(1) から NISHIN(8) に格納される。流れ図のa及びbに入る処理はどれか。ここで，j div 2 はjを2で割った商の整数部分を，j mod 2 はjを2で割った余りを表す。

正解と解説

正解は”エ”

10進数「5」を2進数「00000101」に変換する処理を例にア～エの検証をします。
NISHIN(1) = 1
NISHIN(2) = 0
NISHIN(3) = 1
NISHIN(4~8) = 0
になるはずです。

【アの検証】
・k=1
[a]：5 div 2 = 2 → j
[b]：2 mod 2 = 0 → NISHIN(1)　この時点で違うのでアは×です

【イの検証】
・k=1
[a]：5 mod 2 = 1 → j
[b]：1 div 2 = 0 → NISHIN(1)　この時点で違うのでイは×です

【ウの検証】
・k=1
[a]：5 div 2 = 2 → NISHIN(1)　この時点で違うのでウは×です
[b]：5 mod 2 = 1 → j

【エの検証】
・k=1
[a]：5 mod 2 = 1 → NISHIN(1)
[b]：5 div 2 = 2 → j
・k=2
[a]：2 mod 2 = 0 → NISHIN(2)
[b]：2 div 2 = 1 → j
・k=3
[a]：1 mod 2 = 1 → NISHIN(3)
[b]：1 div 2 = 0 → j
・k=4
[a]：0 mod 2 = 0 → NISHIN(4)
[b]：0 div 2 = 0 → j
これ以降、NISHINには0が入ります。よってエが正しいことが分かります。