この記事では16進数を10進数に変換する方法と10進数を16進数に変換する方法についてIT初心者にも分かりやすく解説します。
16進数を10進数に変換する方法
- 数字の各桁には重みがある。例えば、16進数の1桁目には「1」の重み、2桁目には「16」の重み、3桁目には「256(=16×16)」の重みがある。
- 16進数の数字に各桁の重みを掛けた数字が10進数の数字になる。例えば、16進数の「B1」は1×1+16×11=177となり、10進数に変換した数字は「177」となる。
10進数を16進数に変換する方法
- 10進数の数字を商(答え)が16未満になるまで割り続けて、割り算の余りを繋げた結果が16進数に変換した数字となる。例えば、10進数の「1000」の場合、
①1000÷16=62余り8
②62÷16=3余り14
となり、②の商→②の余り→①の余りを繋げた「3E8」が16進数に変換した後の数字となる。
基本情報では16進数を10進数に変換する問題、10進数を16進数に変換する問題が頻出します。是非最後までご覧ください。
数える時に大切な「位」
10進数の数え方
10進数は0~9の10個の数字を使って数を数えます。10進数では0,1,2,3,4,5,6,7,8,9と10個の数字で1桁の数字を表現した後、2桁目の数を1上げて1桁目の数字を0に戻します。

つまり、2桁目の数字には10個分の数字の重みがあると言えます。もっと分かりやすく飴玉を使って考えてみましょう。例えば、「16」という数字は2桁目が1、1桁目が6です。なので下の画像のように、10個入りの袋が1つとばらの飴玉が6個あるという風に考えることが出来ます。これが、数字の「位」による重みです。
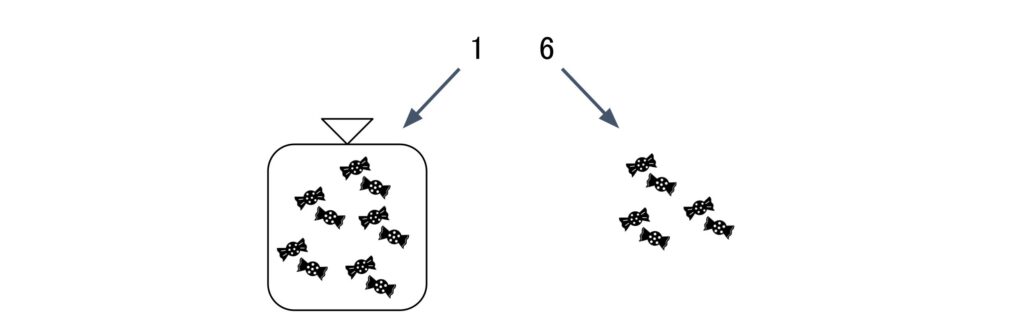
例えば、「234」という数字は3桁目が2、2桁目が3、1桁目が4です。3桁目は10個入りの袋が更に10個入った箱のようなイメージです。10個入りの袋が10個箱に入っているので、3桁目に入っている飴玉は10×10=10²=100個となります。

同じように、4桁目は10個入りの袋が10個入った箱が10個トラックに入っていると考えられるので、4桁目に入っている飴玉は10×10×10=10³=1000個となります。
10進数の位の重み
1桁目・・・10⁰=1(バラの飴玉)
2桁目・・・10¹=10(袋に入った飴玉)
3桁目・・・10²=100(箱に入った飴玉)
4桁目・・・10³=1000(トラックに入った飴玉)
n桁目・・・\( 10^{ n-1} \)
16進数を10進数に変換する
16進数は0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,Fの16個の英数字を使って数を数えます。16進数では16個の英数字で1桁の数字を表現した後、2桁目の数を1上げて1桁目の数字を0に戻します。

2桁目の数字は16個の英数字が積み上がった後に、やっと1つ増やすことが出来ます。つまり、2桁目の数字には16個分の数字の重みがあると言えます。飴玉で例えると、2桁目は飴玉16個入りの袋で、1桁目は飴玉1個のバラになります。なので、例えば、16進数の「14」は飴玉20個分になるので、16進数の「14」=10進数の「20」になります。
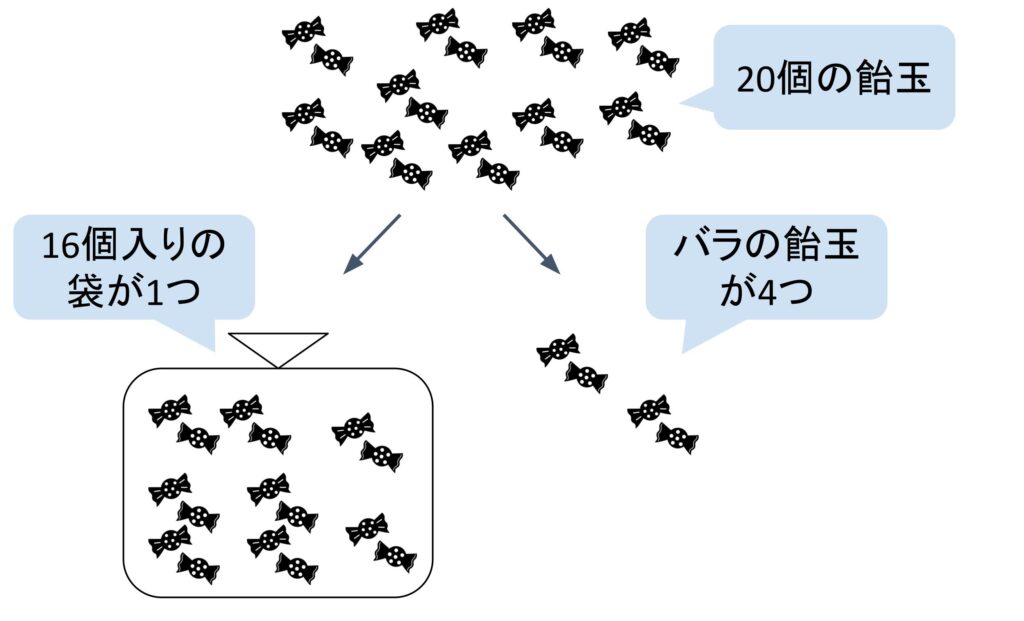
3桁目も10進数と同様に、16個入りの袋が16個入った箱と考えることが出来ます。16進数は使える英数字が0~9とA~Fの16個もあるので、16ずつ位の重みが上がっていくのがポイントです。なので、例えば、16進数の「2B0」は、16²=256個の箱が2つ、16個入りの袋がB(=11個)なので10進数では「688」になります。
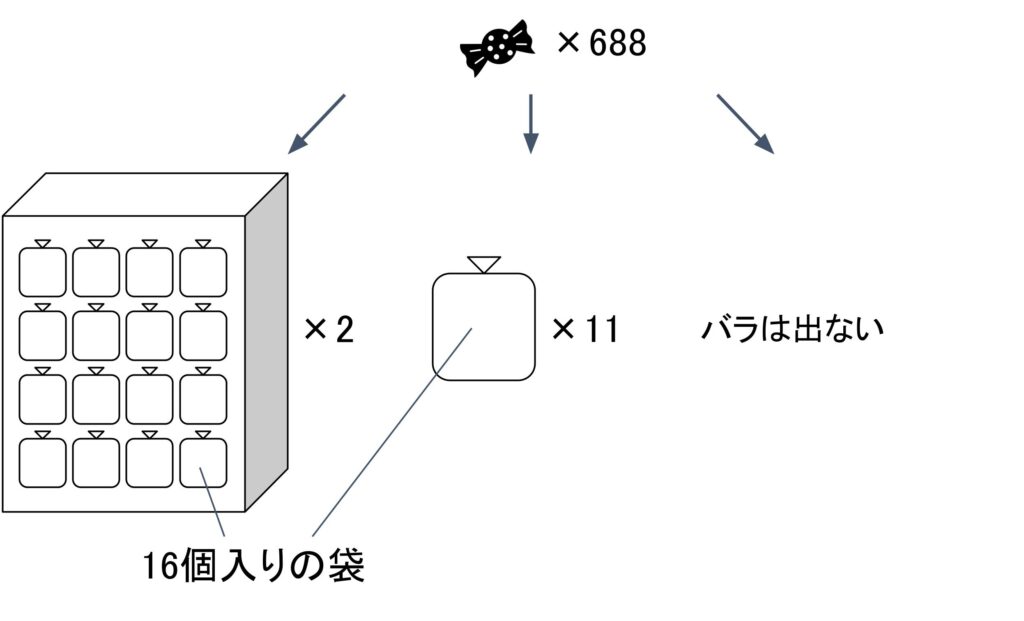
16進数の位の重み
1桁目・・・16⁰=1(バラの飴玉)
2桁目・・・16¹=16(袋に入った飴玉)
3桁目・・・16²=256(箱に入った飴玉)
4桁目・・・16³=4096(トラックに入った飴玉)
n桁目・・・\( 16^{ n-1} \)
16進数を10進数に変換する方法
16進数の位にそれぞれ重みを付けていき、最後に足した数字が10進数となります。例で16進数の「C02A」を10進数に変換します。「C02A」にそれぞれ重みを付けて足し算をすると、49194になるので、2進数の「C02A」は10進数の「49194」であることが分かります。
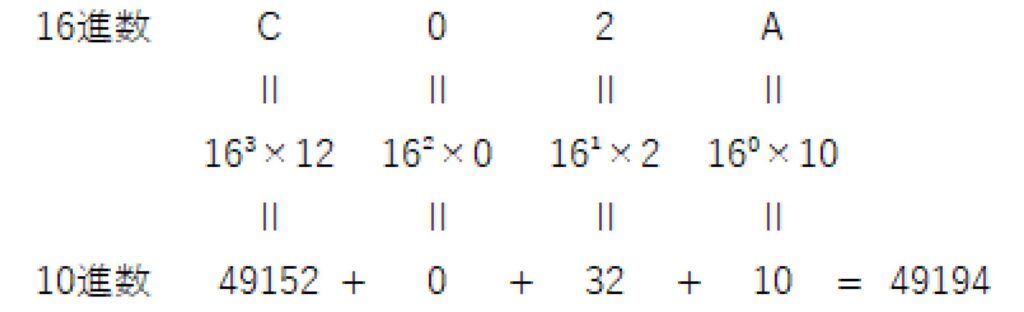
ちなみに小数点以下でも同じことが言えます。
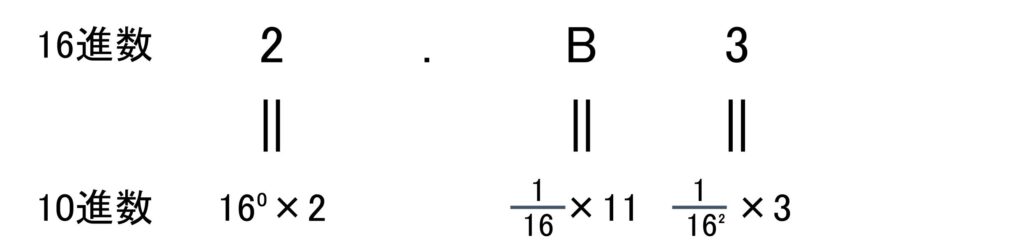
10進数を16進数に変換する
逆に10進数を16進数に変換する方法を考えてみます。先程書いたとおり、16進数の位にはそれぞれ重みがありました。位によって入れることが出来る飴玉の数が違いましたね。
16進数の位の重み
1桁目・・・16⁰=1(バラの飴玉)
2桁目・・・16¹=16(袋に入った飴玉)
3桁目・・・16²=256(箱に入った飴玉)
4桁目・・・16³=4096(トラックに入った飴玉)
n桁目・・・\( 16^{ n-1} \)
10進数の「300」を16進数に変換してみましょう。300個の飴玉を梱包していきます。飴玉が4096個入るトラックだと大きすぎるのでトラックは使えません。飴玉が256個入る箱は使えそうなので箱に梱包します。すると飴玉が44個余ります。次は44個の飴玉を袋に梱包します。16個入りの袋を2つ使って32個の飴玉を梱包します。すると、12個の飴玉が余るので、その飴玉はバラで持ちます。箱は3桁目の重み、袋は2桁目の重み、バラの飴玉は1桁目の重みだったので、10進数の「300」は16進数で「12C」になることが分かります。
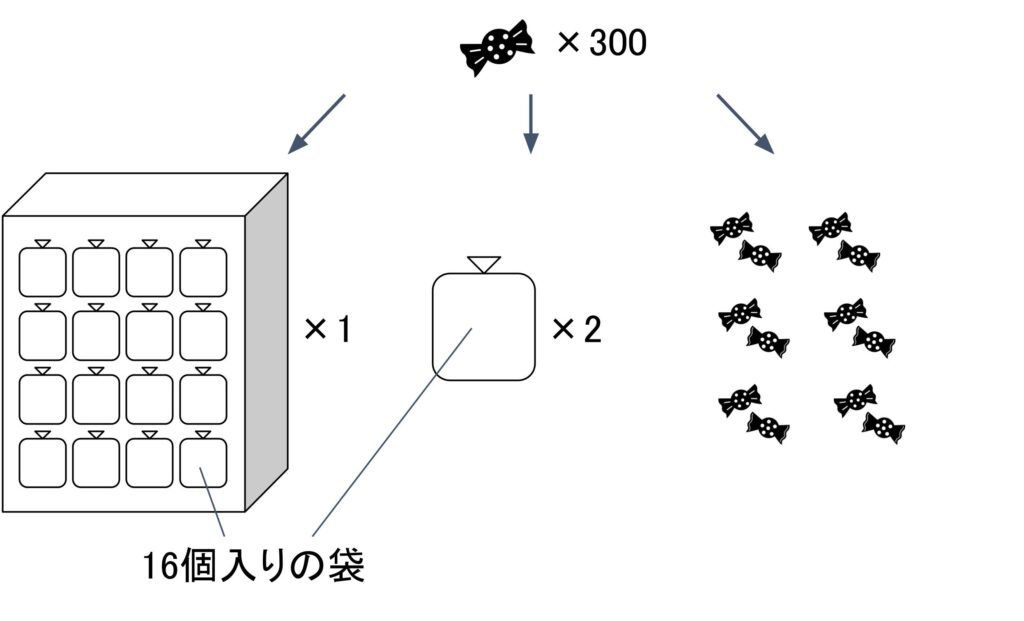
このように、10進数の数を16進数の位の重みで分散させた結果が、16進数で表記した数になります。
10進数を16進数に変換する方法
10進数の数を商が16未満になるまで割り続けて、その余りの数を繋げると16進数になります。例えば下の画像では、10進数の「1000」を16で割り続けて出て来た余りを一番下から繋げ合わせ、16進数で「3E8」と表現できることを示しています。62÷16=3余り14で商は3です。商が16未満なのでここで割り算は終了になります。

(おまけ)10進数を16進数に変換する公式の意味を考える
1000を16進数に変換した例から公式の意味を考えてみたいと思います。
最初に1000÷16=62余り8と求めました。これは、1000個の飴玉を16個入りの袋に梱包していった時に、袋が62個、バラの飴玉が8個発生することを表します。なので、「3E8」の1桁目は8になっているのです。
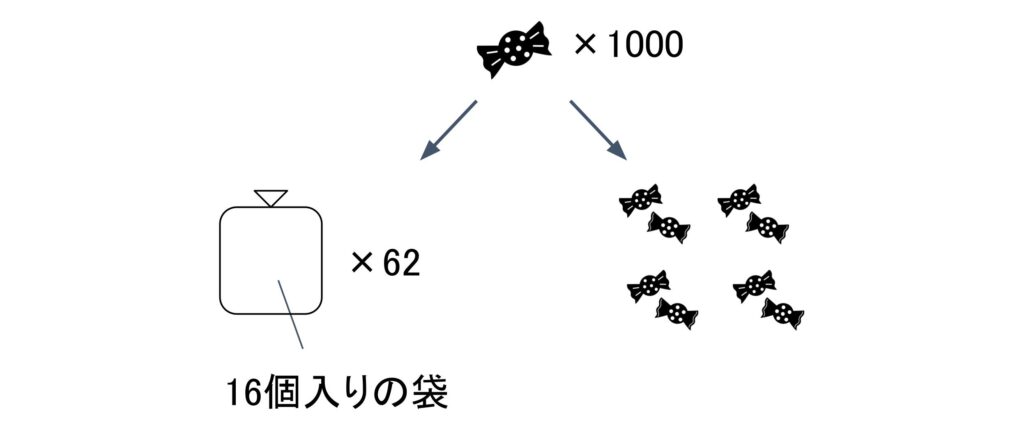
次に62÷16=3余り14と求めました。これは16個入りの袋を16個集めて箱詰めした時に、3個の箱が出来て、14個の袋が余ることを表します。なので、16¹を表す2桁目は14=Eになり、16²を表す3桁目は3になります。箱は3個しか出来なかったので、トラックに積むことは出来ません。
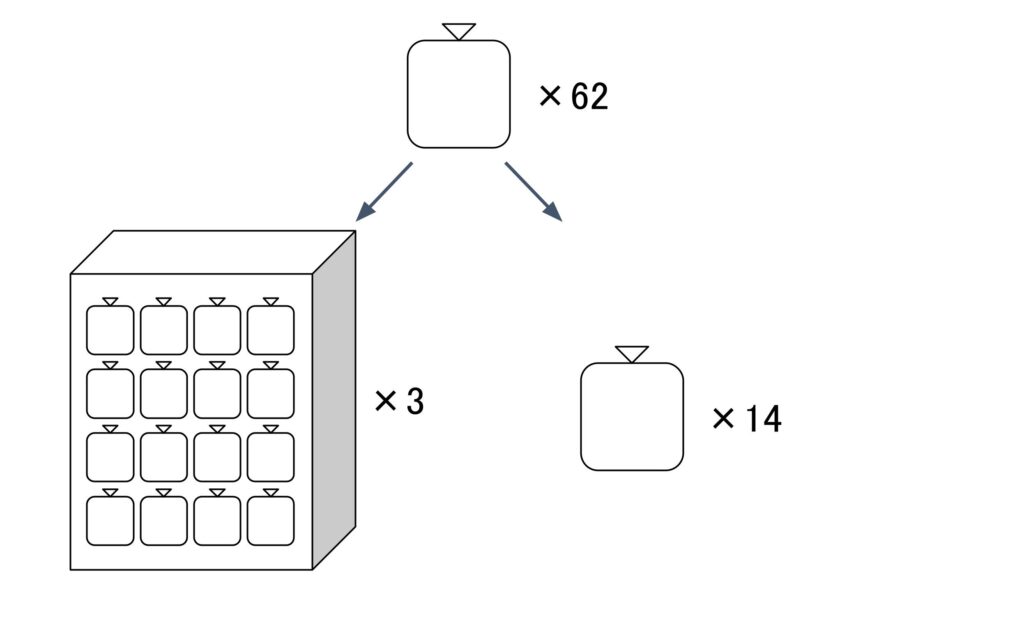
箱は3個しか出来なかったので、トラックに積むことは出来ません。よって、これ以上ペアを作ることは出来ません。
1000=(16²×3)+(16¹×14)+(16⁰×8)となることが分かりました。よって、1000の16進数表現は「3E8」になります。
基本情報技術者試験での出題例
令和5年度問1
基本情報技術者
科目A 令和5年度問1
16進小数0.Cを10進小数に変換したものはどれか。
ア 0.12 イ 0.55 ウ 0.75 エ 0.84
正解は”ウ”
16進数では0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,Fと数が増えます。16進数のCは10進数の12に該当します。なので、0.Cは\(\frac{1}{16}\)×12=0.75となります。
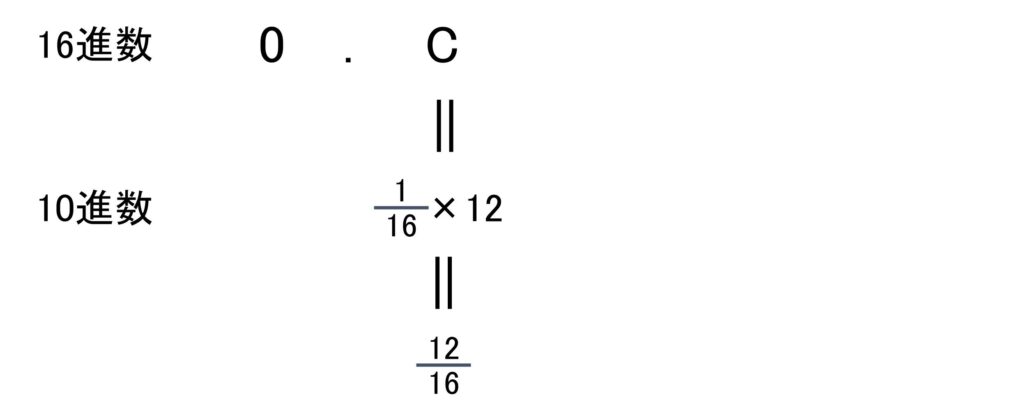
平成30年度秋期問1
基本情報技術者
午前試験 平成30年度秋期問1
16進数の小数0.248を10進数の分数で表したものはどれか。
ア \(\frac{31}{32}\)
ウ \(\frac{31}{512}\)
イ \(\frac{31}{125}\)
エ \(\frac{73}{512}\)
正解は”エ”
16進数「0.248」の各桁の重みはそれぞれ下のようになります。
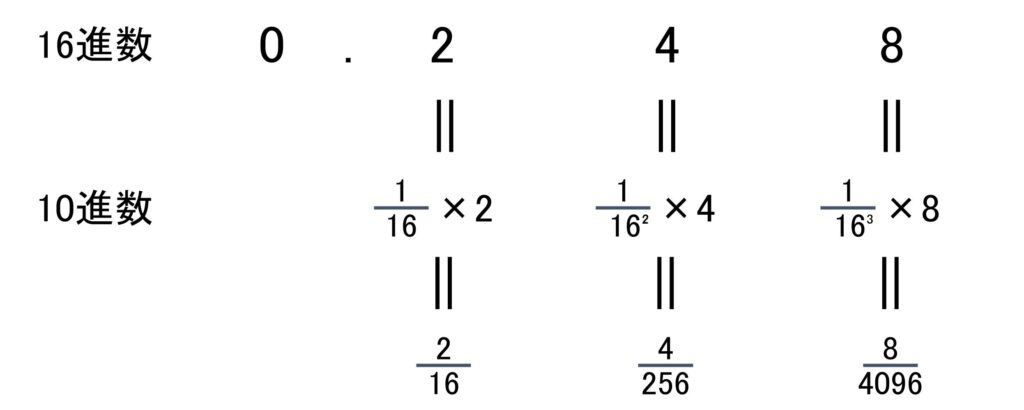
\(\frac{2}{16}\)+\(\frac{4}{256}\)+\(\frac{8}{4096}\)=\(\frac{73}{512}\)となるので、答えはエです。
基本情報に関するの他の記事
| ハードウェア | ソフトウェア | システム構成 |
| ネットワーク | データベース | 開発手法 | 情報セキュリティ |
ハードウェアに関する記事
基数についての記事
【基本情報】コンピュータが理解できるのは0と1だけ?!
【基本情報】2進数と10進数を変換する方法を解説
【基本情報】2の補数について分かりやすく解説!
【基本情報】16進数とコンピュータは相性が良い
【基本情報】16進数と10進数を変換する方法を解説
情報の単位についての記事
【基本情報】ビットとバイトとは何か、1バイト=8ビットの理由も解説
論理演算についての記事
コンピュータの五大装置についての記事
【基本情報】コンピュータってなにで出来ている?-五大装置を解説
【基本情報】クロック周波数とは?なぜ必要なの?
【基本情報】RAMとROMの特徴と違いについて解説
【基本情報】キャッシュメモリについて解説

