【基本情報】16進数と10進数を変換する方法を解説
この記事では、16進数を10進数に、10進数を16進数に変換する方法について、初心者にも分かりやすく、図解付きで丁寧に解説しています!
16進数とは
- 16進数とは0~9とA~Fの16個の英数字で数を表す方法。
- 16進数は2進数と相性が良いため、ITの世界でよく使われる。
16進数を10進数に変換する方法
- 「位の数×格納されている数」をして全部足すと10進数に変換できる。(小数も同じ)
10進数を16進数に変換する方法
- 商が0になるまで16で割って余りを繋げる。
16進数は16個の英数字で数を数える方法
16進数とは、0~9とA~Fの16個の英数字で数を表す方法です。
私たちが普段使う10進数では、0から9までの10個の数字で数を表します。
10進数:10個の数字で数を表す
⇒ 0,1,2,3,4,5,6,7,8,9
16進数:16個の英数字で数を表す
⇒0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
10進数では、「9」の次は「10」です。「9」より大きい1桁の数字は無いので、桁上がりして「10」になるんですね。
一方、16進数では、「9」の次は「A」になり、「F」の次が「10」になります。
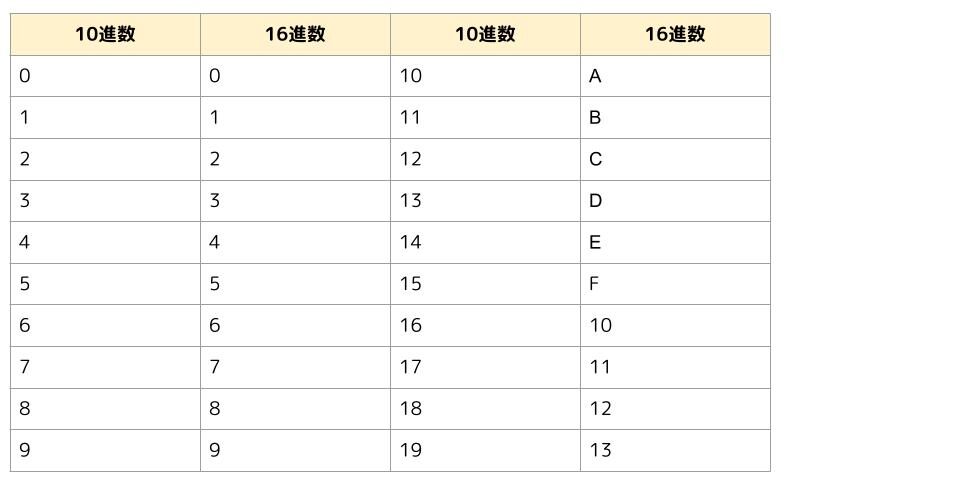
10進数と16進数の対応表は下のようになります。
10進数の「16」は16進数の「10」ということですね。
なぜ16進数を勉強するのか
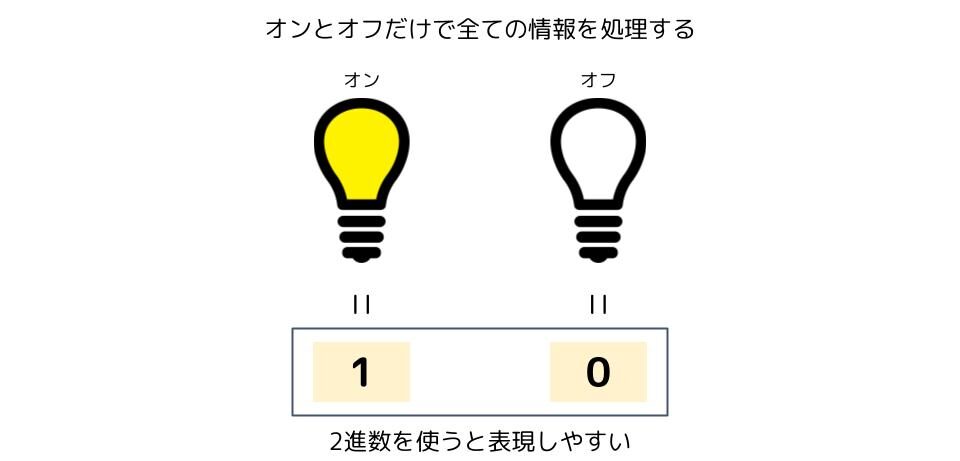
コンピュータは電子機器です。なので、電気を使って様々な処理をしています。
電気にはオンとオフの2つの状態しかありません。この2つの状態を「1」と「0」で表現するのが便利なので、「1」と「0」で数を表す2進数がコンピュータでは使われています。
しかし、2進数で使える数は0と1だけなので、桁数が大きくなりがちなんですね。
例えば、10進数の「100」は2進数で「1100100」と表現します。10進数なら3桁で表現出来た情報を2進数で表現するには7桁も必要です。
我々人間からすると、桁数が大きくなるほど、読み間違えも増えそうでちょっと嫌だなと思いますよね。
ここで出てくるのが16進数です。
下の表を見てください。4桁の2進数と1桁の16進数が綺麗に対応しています。
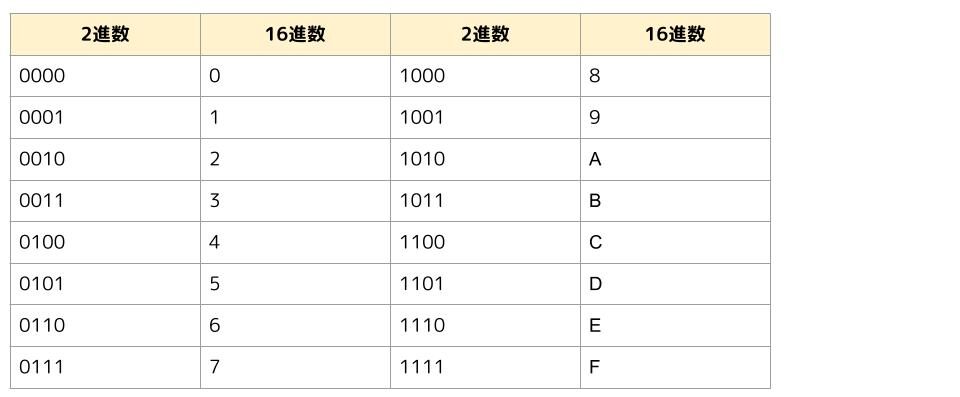
2進数で表現しているものを、4桁区切りで綺麗に変換出来るから16進数は便利で、よく使われるんですね。
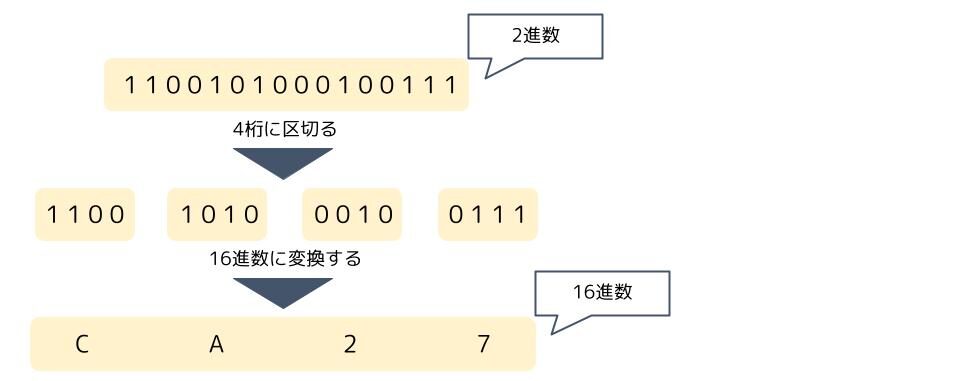
これがITで16進数を勉強する理由です。
16進数を10進数に変換する方法
16進数を10進数に変換する方法を学ぶ前提として、位取り記数法の考え方を知って欲しいと思います。難しい名前ですが、実は私たちは普段、位取り記数法で数を表現しています。
例えば、10進数で「2356」と記載があれば、1000が2つ、100が3つ、10が5つ、1が6つあることを表しています。位は10倍ずつ上がっていくので、右から4つ目の位は1000の位で、そこにある「2」は「2000」を意味すると無意識で理解しています。この考え方が位取り記数法です。
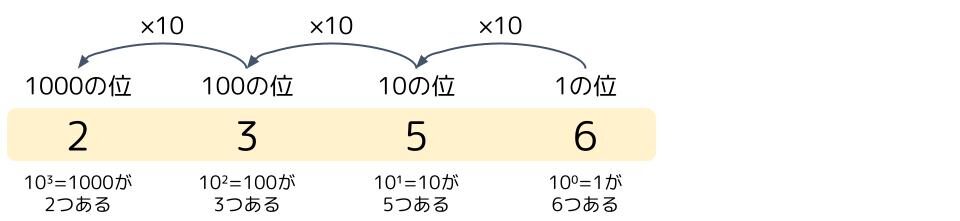
では、16進数の場合はどうなるでしょうか?
16進数の場合も同じように考えます。「2A5F」と記載があれば、4096が2つ、256が10つ、16が5つ、1が15つあることを表しています。16進数の場合、位は16倍ずつ上がっていくので、右から4つ目の位は4096の位で、そこにある「2」は「4096×2=8192」を意味します。同じように全ての桁の値を考えていくと、16進数の「2A5F」は10進数の「10847」だと計算出来ます。これが16進数を10進数に変換する方法です。
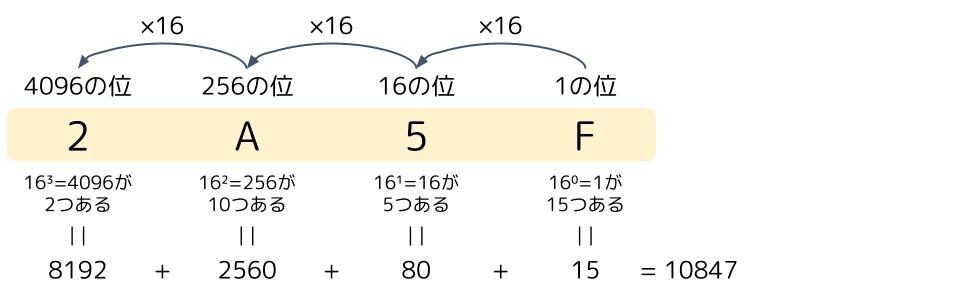
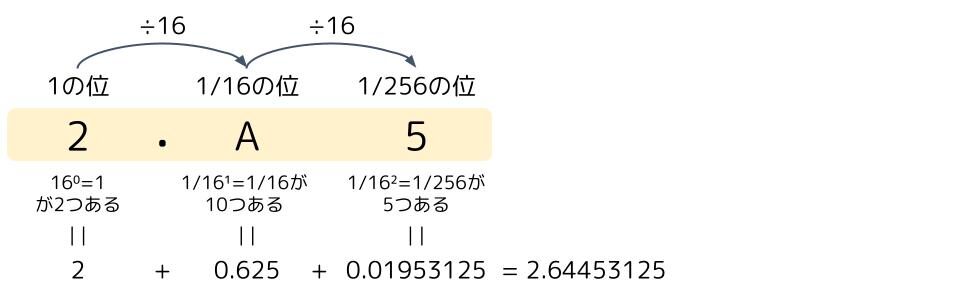
ちなみに、これは小数でも同じことが言えますね。
1の位の右隣は、1を16で割った1/16の位で、その右隣は1/256の位になります。
1/256の位にある「5」は「1/256×5=5/256」を意味します。
10進数を16進数に変換する方法
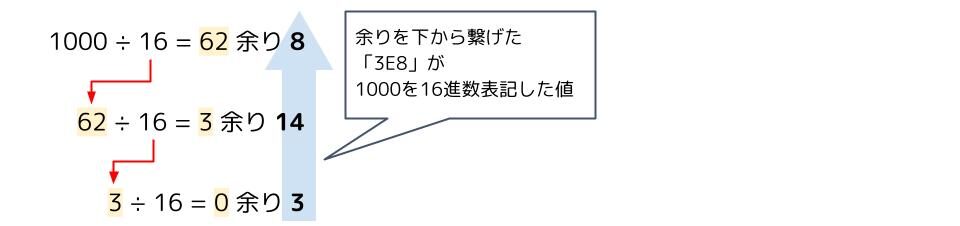
10進数を16進数に変換するには、ひたすら16で割って余りを繋げます。
実際に10進数の「1000」を16進数に変換してみましょう。
- 「1000」を16で割る。1000÷16=62余り8
- ①の商である「62」を16で割る。62÷16=3余り14
- ②の商である「3」を16で割る。3÷16=0余り3
- 商が「0」になったので16で割るのはここで終わり。
- 余りを下から繋げると「3E8」となる。
ただし、10進数の「14」=16進数の「E」であることに注意!
これが「1000」を16進数表記した値になる。
なぜ上の方法で10進数を16進数に変換出来るのか
「1000」を16で割り続ける操作を図にしてみましょう。
「1000÷16=62余り8」は1000個の玉で16個1組のペアを作るとき、62個の箱が出来て、8個玉が余ることを意味します。
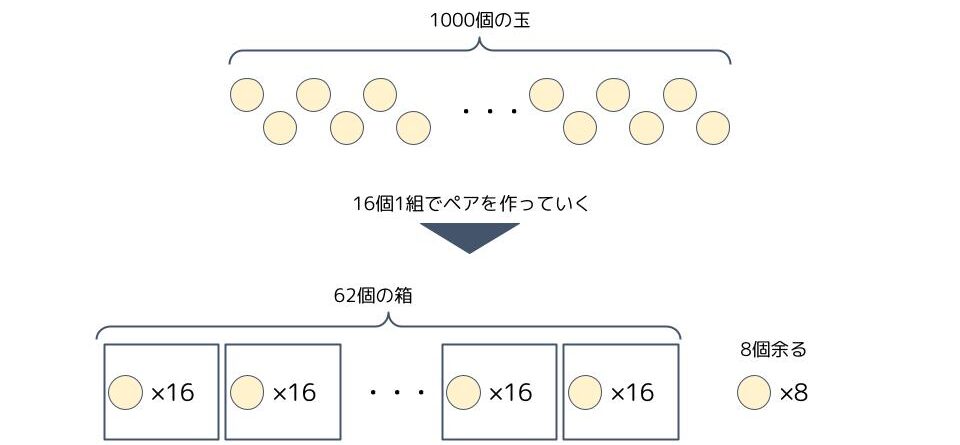
次の「62÷16=3余り14」は上で作った16個入りの箱で、更に16箱1組のペアを作るとき、3個の箱が出来て、14箱余ることを意味します。
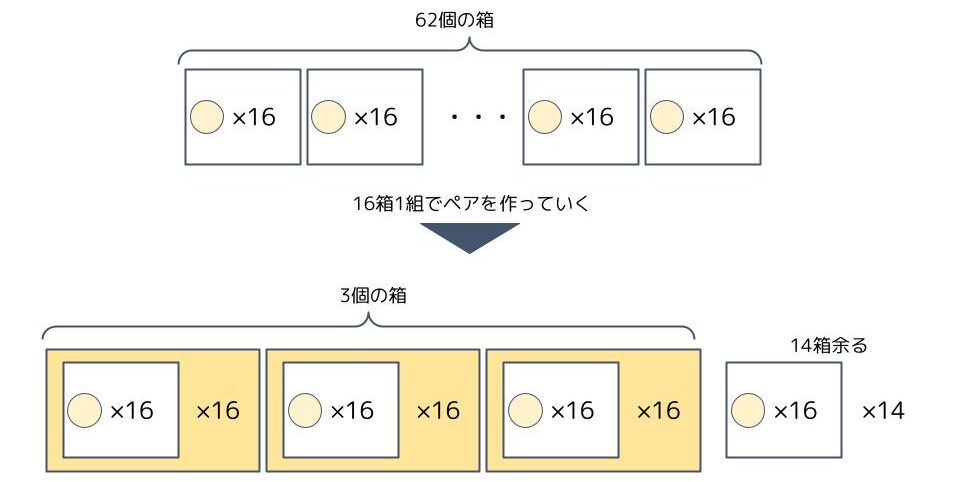
最後の「3÷16=0余り3」は上で作った16×16=256個入りの箱で、更に16箱1組のペアを作るとき、ペアは出来ずに、3箱余ることを意味します。
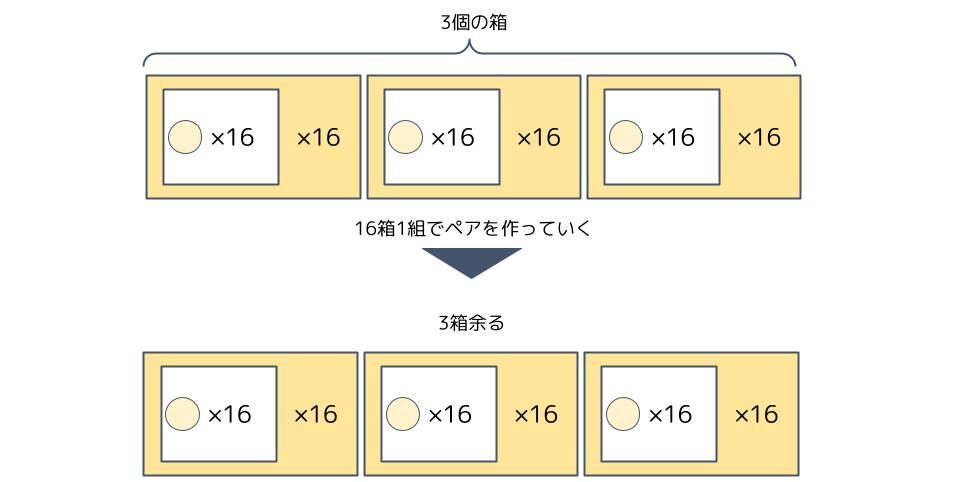
以上のことから、「1000」個の玉をそれぞれの箱に振り分けていくと、
「256(=16²)個入りの箱」が3箱、「16個入りの箱」が14箱、玉の余りが8個出ることが分かりました。なので、10進数の「1000」を16進数に変換すると、256の位に「3」、16の位に「E(=14)」、1の位に「8」の「3E8」になる訳ですね。
基本情報技術者試験での出題例
令和5年度問1
基本情報技術者
科目A 令和5年度問1
16進小数0.Cを10進小数に変換したものはどれか。
ア 0.12 イ 0.55 ウ 0.75 エ 0.84
正解は”ウ”
16進数では0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,Fと数が増えます。16進数のCは10進数の12に該当します。なので、0.Cは\(\frac{1}{16}\)×12=0.75となります。

平成30年度秋期問1
基本情報技術者
午前試験 平成30年度秋期問1
16進数の小数0.248を10進数の分数で表したものはどれか。
ア \(\frac{31}{32}\)
ウ \(\frac{31}{512}\)
イ \(\frac{31}{125}\)
エ \(\frac{73}{512}\)
正解は”エ”
16進数「0.248」の各桁の重みはそれぞれ下のようになります。
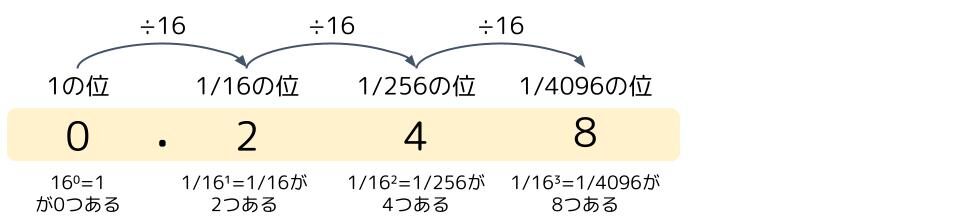
\(\frac{2}{16}\)+\(\frac{4}{256}\)+\(\frac{8}{4096}\)=\(\frac{73}{512}\)となるので、答えはエです。



