この記事ではアルゴリズムについてIT初心者にも分かりやすく解説します。
アルゴリズム
- アルゴリズムは特定の問題を解決するための手順。
- フローチャートはアルゴリズムを図式化したもの。
- アルゴリズムの問題を解く時は、
①具体的な数字を使って考える
②処理と判断に注目する
③1Stepずつ丁寧に見る
基本情報ではアルゴリズムに関する問題が出題されます。是非最後までご覧ください。
アルゴリズムとは?
アルゴリズムとは特定の問題を解決するための決められた手順のことです。
銭湯を例にアルゴリズムの存在意味を考えてみましょう。
ある銭湯では「親が同伴の場合は子供の混浴OK」というルールがあります。しかし、子供とはどれくらいの子供のことを指すのでしょうか?人によって、何歳まではOKとか、身長何cm以下まではOKとか基準が違いますよね。なので決められた手順を作り、誰が判断しても同じ答えになるようにします。この決められた手順のことをアルゴリズムと言います。

コンピュータにして欲しい処理を記述することをプログラミングと言いますが、プログラミングをする際、どのような手順でコンピュータに処理をしてもらうのかを考える必要があります。なので、アルゴリズムを考えることはプログラミングをする上でとても重要です。
フローチャートとは?
フローチャートとはアルゴリズムを図で表したものです。
もう少し複雑なアルゴリズムで例を見てみましょう。「1~10の整数のうち、偶数の合計はいくらになるのか?」という問題を解く手順をフローチャートで表現すると下図のようになります。
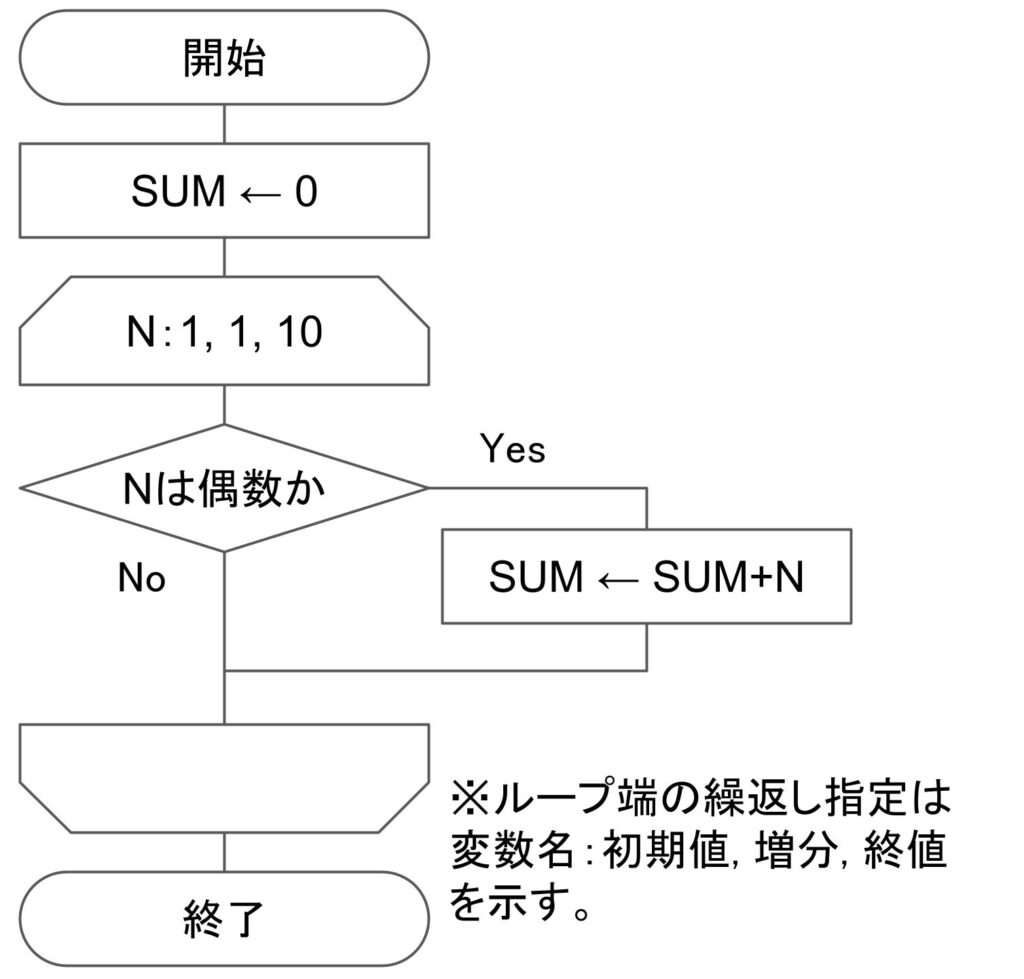
順を追ってこのフローチャートを解説していきます。
変数
変数とは数字や文字列等のデータを格納する箱のようなものです。上のフローチャートで言うとNやSUMが変数に当たります。
変数を用意する時は、「変数の名前」と「変数に格納するデータ型」の2つを必ず決めます。
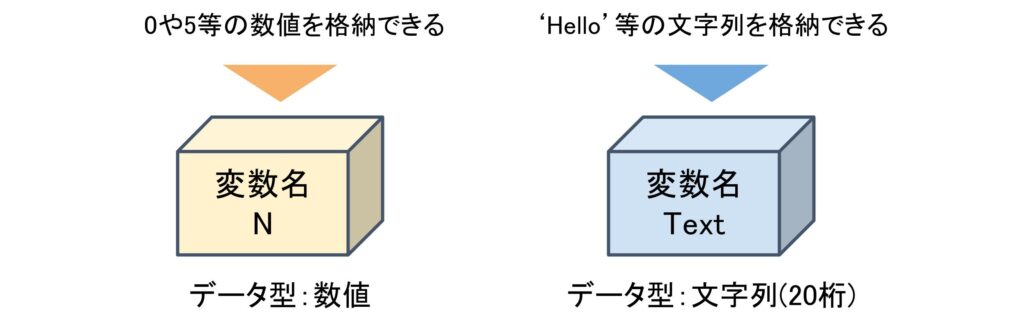
変数という箱を用意したらデータを格納する必要があります。
変数に値Xを格納するのをフローチャートでは「変数名 ← X」と表記します。
数値5を変数Nに代入する
・N ← 5
また、変数に格納された数値を編集する、例えば変数にXを足す場合は
「変数名 ← 変数名 + X」と表記します。
【例】
①数値5を変数Nに代入する
・N ← 5
②変数Nに3を加える
・N ← N + 3
②の「N ← N + 3」でNが2個出てきていますが、この2つのNに入っている値は異なります。「←」の先にあるNは処理を行った後のNで、「←」の元にあるNは処理を行う前のNです。なので分かりやすく記載すると「N(処理後) ← N(処理前) + 3」になります。
処理前のNは①で代入された5で、処理後のNは処理前のNに3を足した8になるので、②が終わった時点で、Nは8になりますね。
「←」の前後で同じ変数が記載されている場合
←の先にある変数:処理後の変数
←の元にある変数:処理前の変数
また、値の代入を行うとき、複数の変数が絡んでくることがあります。
【例】
①数値5を変数Nに代入する
・N ← 5
②数値4を変数Mに代入する
・M ← 4
③変数Nから変数Mを引く
・N ← N – M
←の元にある変数は処理前の変数、←の先にある変数は処理後の変数でした。なので、③は「N(処理後:1) ← N(処理前:5) – M(処理前:4)」になり、③が終わった時点で、Nは1になります。
フローチャートで使う記号
フローチャートでは主に下の4つ記号を使います。
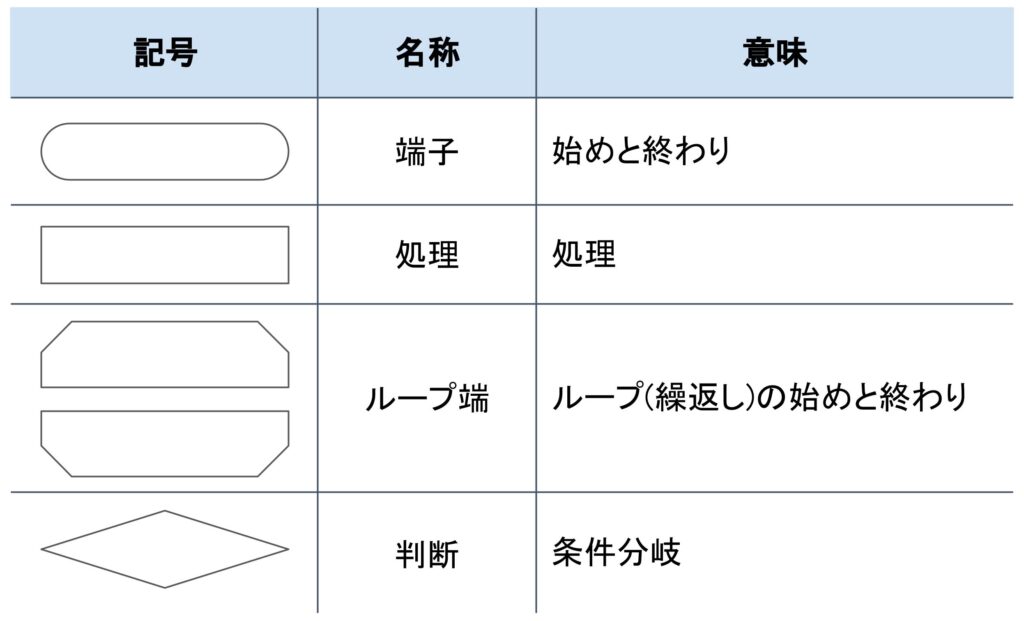
正直、端子と処理は見れば分かると思うので、判断とループ端について説明します。
判断
判断は条件によって処理を変えたい場合に使います。
「1~10の整数のうち、偶数の合計はいくらになるのか?」の問題では、整数が偶数なのかどうかという条件によって処理を変えています。これを判断の記号で表現すると下図のようになります。
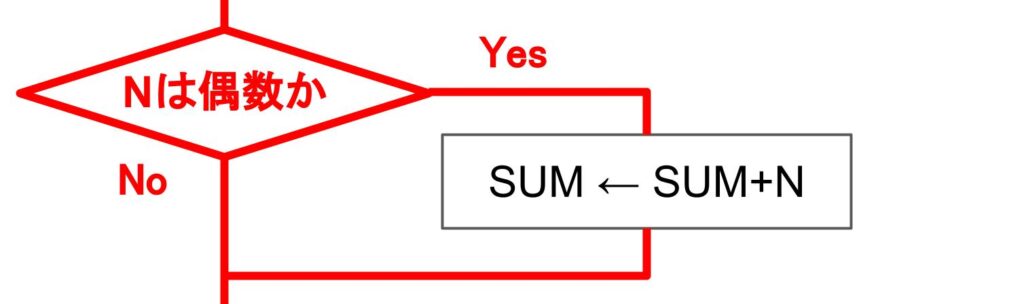
- 整数Nが偶数の場合(Yes)は、合計値を入れる変数SUMにNを加える処理を行う
- 整数Nが偶数ではない場合(No)は、何もしない
ということがフローチャートから分かりますね。
ループ端
ループ端は繰返し処理を表現したい場合に使います。
「1~10の整数のうち、偶数の合計はいくらになるのか?」の問題では、
- 1は偶数ではないので、何もしない
- 2は偶数なので、足し算をする
- 3は偶数ではないので、何もしない
- 4は偶数なので、足し算をする
というように、「1~10まで、整数が偶数なのかどうか見て、偶数ならば足し算をして偶数でなければ何もしない」ことを繰り返しています。これをループ端の記号で表現すると下図のようになります。
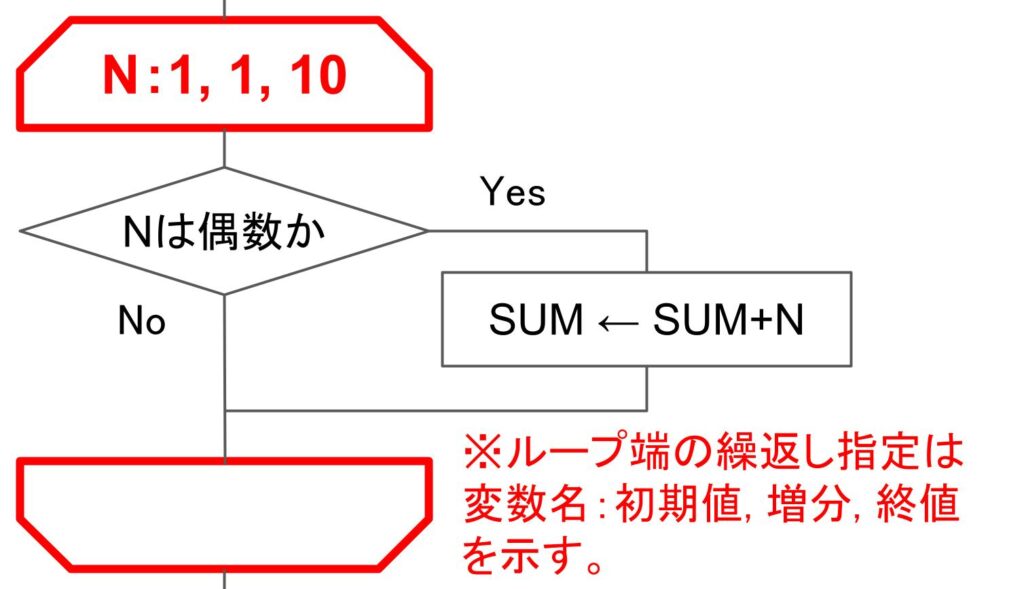
ループ端を使う場合、どういう条件で繰返し処理を行うのかを記載する必要があります。
今回の例で言うと、「N:1,1,10」が繰返し処理の条件になります。フローチャートの補足に説明がありますが、これらの数字はそれぞれ「N:1(初期値),1(増分),10(終値)」の意味を持ちます。
初期値と終値はその名の通り、繰返し処理開始時のNの値と終了時のNの値を表します。
今回の問題では1~10までの整数を見ているので、初期値=1、終値=10になります。
増分はNが初期値から終値まで何ずつ増えていくのかを表します。
今回の問題では1~10までの整数を1ずつ見ているので、増分=1になります。
【繰返し条件の例】
① N:1,1,10
「1,2,3,・・・9,10」のように、1~10まで1ずつ整数を見ていく。
② N:0,5,100
「0,5,10,15,・・・95,100」のように、0~100まで5ずつ整数を見ていく。
③ N:30,-3,0
「30,27,24,21,・・・3,0」のように、30~0まで3ずつ減らしながら整数を見ていく。
改めて問題を見てみる
改めて「1~10の整数のうち、偶数の合計はいくらになるのか?」のフローチャートを見てみましょう。

最初SUMに0を代入し、その後、繰返し処理を行っています。
繰返し処理の中ではNが偶数かどうかを見ており、Nが偶数の場合はSUMにNを加えて、Nが偶数でない場合は何もしません。
この繰返し処理をN=1(初期値)~10(終値)まで、Nの値を1(増分)ずつ増やしながら見ています。N=10の時の処理が終わったらプログラムは終了です。最終的にNとSUMに入っている値は、N=10,SUM=30となり、合計値が30であると分かります。
アルゴリズムの苦手意識をなくす方法
特にIT未経験者にとってアルゴリズムの問題は取っ掛かり辛く、苦手意識が芽生えやすい分野かなと思います。(私はIT未経験の大学生の時に基本情報を取りましたが、アルゴリズムが一番苦手でした、、、)
アルゴリズムの問題を解くコツは、この3点だと思います。
- 具体的な数字を使ってアルゴリズムを解く
- 処理と判断に注目する
- 1Stepずつ丁寧に見る
このコツについて実際の過去問を使って解説していきます。
基本情報技術者試験での出題例
サンプル問題問2、令和元年度秋期問1
基本情報技術者
科目A サンプル問題問2、午前試験 令和元年度秋期問1
次の流れ図は,10進整数j(0<j<100)を8桁の2進数に変換する処理を表している。2進数は下位桁から順に,配列の要素NISHIN(1)からNISHIN(8)に格納される。流れ図のa及びbに入れる処理はどれか。ここで,j div 2はjを2で割った商の整数部分を,j mod 2はjを2で割った余りを表す。

正解は”エ”
【アルゴリズム問題の鉄則①:具体的な数字を使う】
今回は10進数を2進数に変換するアルゴリズムなので、例えば「5」を2進数に変換する場合を考えてみましょう。
「5」を2進数に変換すると「00000101」になります。
「2進数は下位桁から順に,配列の要素NISHIN(1)からNISHIN(8)に格納される。」と書いてあるので、
・NISHIN(1)=1
・NISHIN(2)=0
・NISHIN(3)=1
・NISHIN(4)=0
・NISHIN(5)=0
・NISHIN(6)=0
・NISHIN(7)=0
・NISHIN(8)=0
になるはずです。
【アルゴリズム問題の鉄則②:処理と判断に着目する】
今回は判断が無いので、処理にそれぞれ処理①~処理③と名前を付けていきます。

【アルゴリズム問題の鉄則③:1Stepずつ丁寧に見る】
処理①:jに「5」を入力
[kを1~8まで、1ずつ増やしながら処理②と処理③を行う]
●k=1のとき
処理②
ア:j ← j div 2なので処理②が終わった後は、j = 2
イ:j ← j mod 2なので処理②が終わった後は、j = 1
ウ:NISHIN(k) ← j div 2なので処理②が終わった後は、NISHIN(1) = 2
エ:NISHIN(k) ← j mod 2なので処理②が終わった後は、NISHIN(1) = 1
処理③
ア:NISHIN(k) ← j mod 2なので処理②が終わった後は、NISHIN(1) = 0
イ:NISHIN(k) ← j div 2なので処理②が終わった後は、NISHIN(1) = 0
ウ:j ← j mod 2なので処理②が終わった後は、j = 1
エ:j ← j div 2なので処理②が終わった後は、j = 2
k=1の処理が終わった段階でNISHIN(1) = 1となっているのはエだけなので、
答えは’エ’になります。答えは分かりましたが、折角なのでk=4くらいまで見てみましょう。
◎k=1終了時点(正解のエのパターンだけ記載)
j = 2
NISHIN(1) = 1
●k=2のとき
処理②
エ:NISHIN(k) ← j mod 2なので処理②が終わった後は、NISHIN(2) = 0
処理③
エ:j ← j div 2なので処理②が終わった後は、j = 1
◎k=2終了時点
j = 1
NISHIN(2) = 0
●k=3のとき
処理②
エ:NISHIN(k) ← j mod 2なので処理②が終わった後は、NISHIN(3) = 1
処理③
エ:j ← j div 2なので処理②が終わった後は、j = 0
◎k=3終了時点
j = 0
NISHIN(3) = 1
●k=4のとき
処理②
エ:NISHIN(k) ← j mod 2なので処理②が終わった後は、NISHIN(4) = 0
処理③
エ:j ← j div 2なので処理②が終わった後は、j = 0
◎k=3終了時点
j = 0
NISHIN(4) = 0
この時点でj=0なので、これ以降はずっとNISHIN(k) = 0になります。
サンプル問題問6、令和元年度秋期問9
基本情報技術者
科目A サンプル問題問6、午前試験 令和元年度秋期問9
配列Aが図2の状態のとき,図1の流れ図を実行すると,配列Bが図3の状態になった。図1のaに入れる操作はどれか。ここで,配列A,Bの要素をそれぞれ A(i,j),B(i,j) とする。
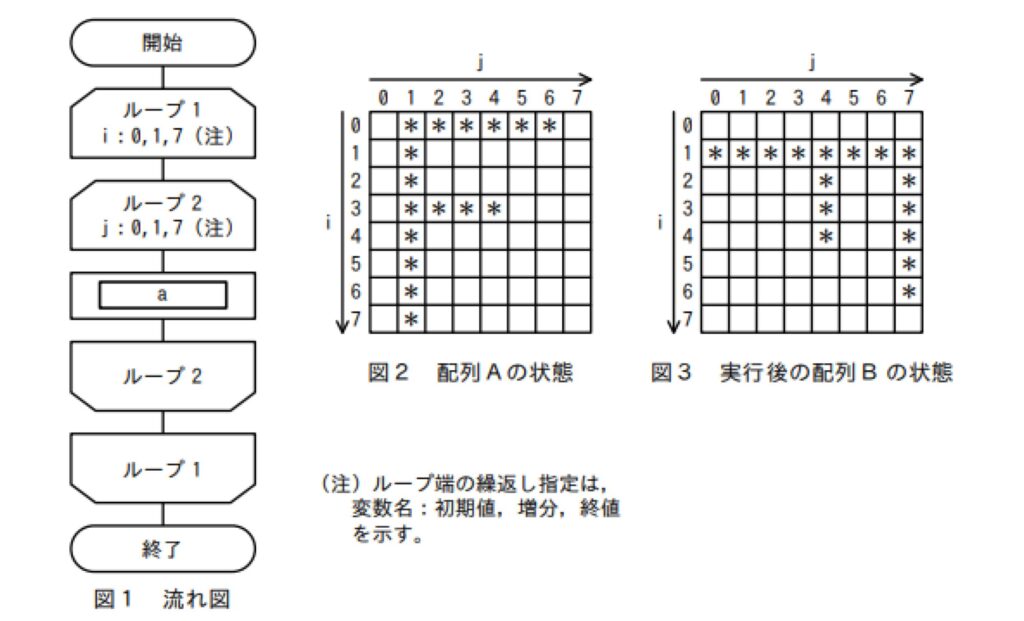
ア B (7-i, 7-j) ← A (i, j)
ウ B (i, 7-j) ← A (i, j)
イ B (7-j, i) ← A (i, j)
エ B (j, 7-i) ← A (i, j)
正解は”エ”
【アルゴリズム問題の鉄則①:具体的な数字を使う】
今回の問題では具体的な数字を入力する変数が無いので鉄則①は飛ばします
【アルゴリズム問題の鉄則②:処理と判断に着目する】
今回は判断が無いので、処理にそれぞれ名前を付けていきます。
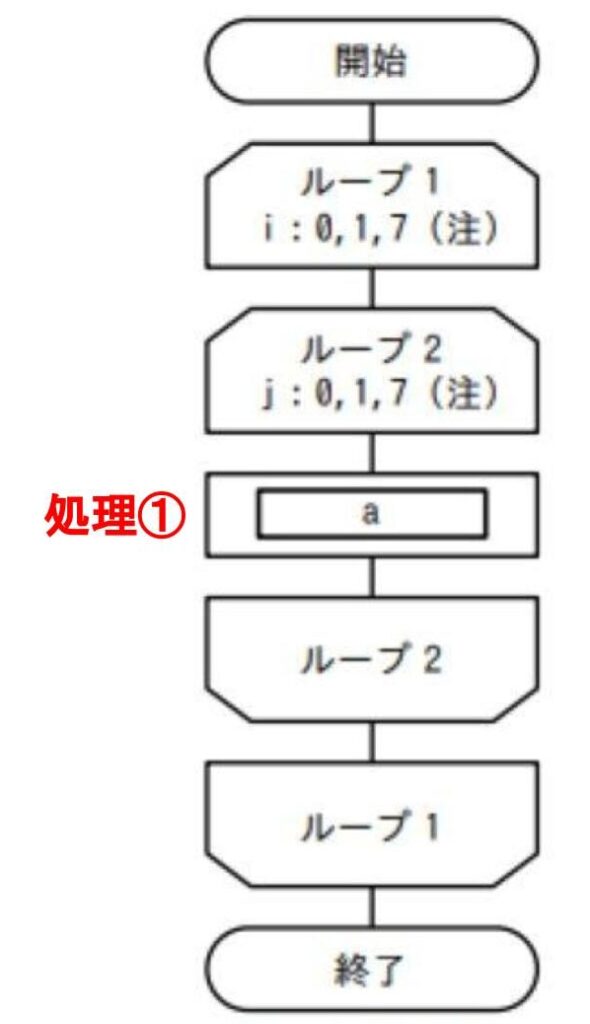
【アルゴリズム問題の鉄則③:1Stepずつ丁寧に見る】
この問題ではiを条件とした繰返し処理の中にjを条件とした繰返し処理が入っています。
この場合、i=0のときのj=0~7を考え、次にi=1のときのj=0~7を考え、次にi=2のときのj=0~7を考え、、、という風にアルゴリズムを解きます。
●i=0のとき
・j=0のとき、処理①
・j=1のとき、処理①
・j=2のとき、処理①
:
:
・j=7のとき、処理①
●i=1のとき
・j=0のとき、処理①
・j=1のとき、処理①
・j=2のとき、処理①
:
:
・j=7のとき、処理①
●i=2のとき
・j=0のとき、処理①
・j=1のとき、処理①
・j=2のとき、処理①
:
:
・j=7のとき、処理①
それでは実際にアルゴリズムを見ていきましょう。
●i=0のとき
・j=0のとき
処理①
ア:B (7-i, 7-j) ← A (i, j)なのでA(0,0)がB(7,7)に移動
イ:B (7-j, i) ← A (i, j)なのでA(0,0)がB(7,0)に移動
ウ:B (i, 7-j) ← A (i, j)なのでA(0,0)がB(0,7)に移動
エ:B (j, 7-i) ← A (i, j)なのでA(0,0)がB(7,7)に移動
A(0,0)には「*」が入っていないので移動先のBにも「*」は入りません。
図3を見るとB(0,7)、B(7,0)、B(7,7)に「*」は入っていません。
なので、この時点ではア~エ全てOKです。
・j=1のとき
処理①
ア:B (7-i, 7-j) ← A (i, j)なのでA(0,1)がB(7,6)に移動
イ:B (7-j, i) ← A (i, j)なのでA(0,1)がB(6,0)に移動
ウ:B (i, 7-j) ← A (i, j)なのでA(0,1)がB(0,6)に移動
エ:B (j, 7-i) ← A (i, j)なのでA(0,1)がB(1,7)に移動
A(0,1)には「*」が入っているので移動先のBにも「*」は入ります。
図3を見るとB(1,7)だけ「*」が入っています。
なので、この時点ではエが正解だと分かります。
令和5年度問11
基本情報技術者
午前試験 令和5年度問11
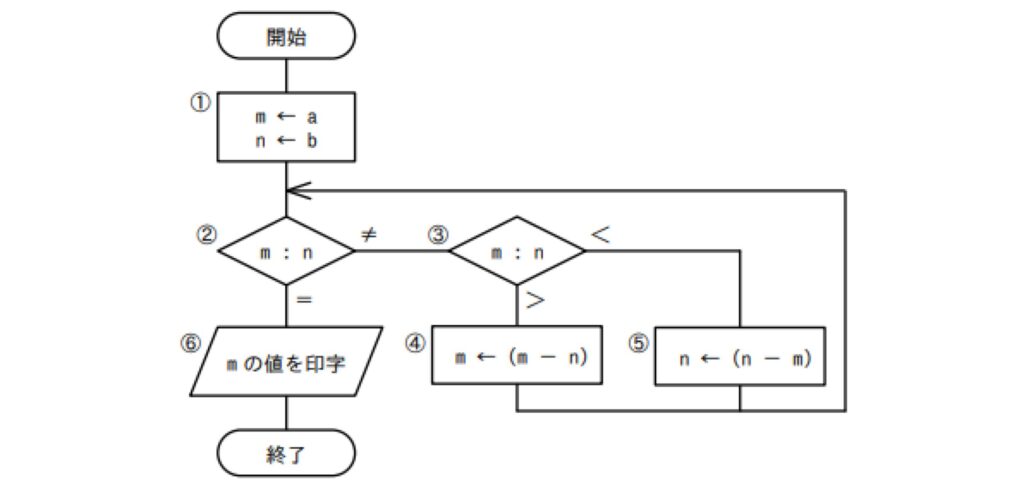
次の流れ図において,
①→②→③→⑤→②→③→④→②→⑥
の順に実行させるために,①においてmとnに与えるべき初期値aとbの関係はどれか。ここで,a,bはともに正の整数とする。
ア a = 2b
ウ 2a = 3b
イ 2a = b
エ 3a = 2b
正解は”エ”
【アルゴリズム問題の鉄則①:具体的な数字を使う】
今回の問題ではア~エで初期値が異なるのでそれぞれで具体例を設定します。
ア a=2, b=1
イ a=1, b=2
ウ a=3, b=2
エ a=2, b=3
【アルゴリズム問題の鉄則②:処理と判断に着目する】
今回は問題の中で処理と判断に名前が付けられていますので、それを流用しましょう。

【アルゴリズム問題の鉄則③:1Stepずつ丁寧に見る】
処理①:mとnにそれぞれaとbを代入する
ア a=2, b=1としたので、m=2, n=1
イ a=1, b=2としたので、m=1, n=2
ウ a=3, b=2としたので、m=3, n=2
エ a=2, b=3としたので、m=2, n=3
判断②:mとnが同値かどうか
ア m=2, n=1なので、≠
イ m=1, n=2なので、≠
ウ m=3, n=2なので、≠
エ m=2, n=3なので、≠
判断③:mとnの大小比較
ア m=2, n=1なので、>
イ m=1, n=2なので、<
ウ m=3, n=2なので、>
エ m=2, n=3なので、<
この問題では「①→②→③→⑤→②→③→④→②→⑥」の順に実行する組み合わせを探しています。判断③の次に処理⑤に行くのは「<」のパターンです。
よって、この時点で答えはイかエに絞れます。ここからはイとエだけを見ていきましょう。
処理⑤:n ← (n-m)
イ m=1, n=2なので、n=1になる
エ m=2, n=3なので、n=1になる
判断②:mとnが同値かどうか
イ m=1, n=1なので、=
エ m=2, n=1なので、≠
「①→②→③→⑤→②→③→④→②→⑥」の順に実行するので、2回目の判断②の次は判断③です。判断③に行くのは≠の時なので、この時点で答えはエになります。答えは分かりましたが、最後まで見てみましょう。
判断③:mとnの大小比較
エ m=2, n=1なので、>
処理④:m ← (m-n)
エ m=2, n=1なので、m=1になる
判断②:mとnが同値かどうか
エ m=1, n=1なので、=
出力⑥:mの値を印字
平成31年度春期問7
基本情報技術者
午前試験 平成31年度春期問7
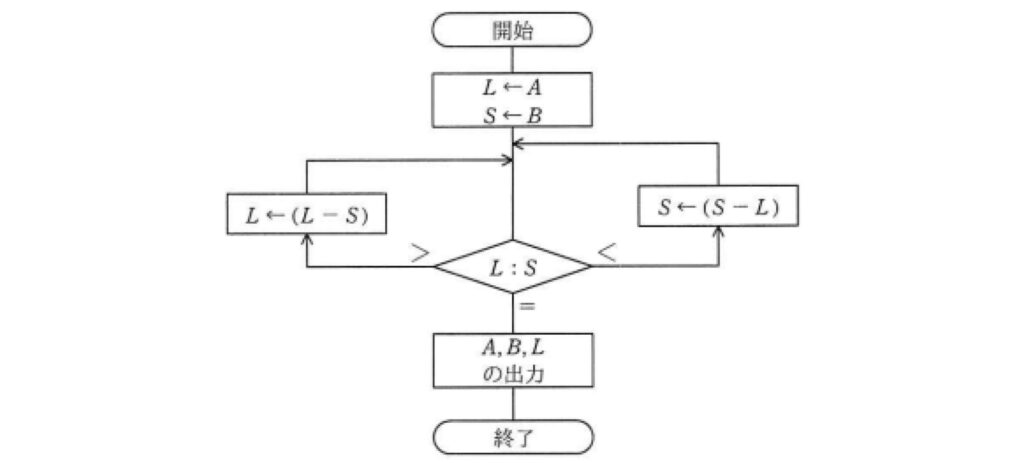
次の流れ図は,2数 A,B の最大公約数を求めるユークリッドの互除法を,引き算の繰返しによって計算するものである。Aが876,Bが204のとき,何回の比較で処理は終了するか。
ア 4
ウ 10
イ 9
エ 11
正解は”エ”
【アルゴリズム問題の鉄則①:具体的な数字を使う】
今回の問題では具体的な数字が与えられていますね。
A=876
B=204
【アルゴリズム問題の鉄則②:処理と判断に着目する】
下の画像のように処理と判断に名前を付けてみます。
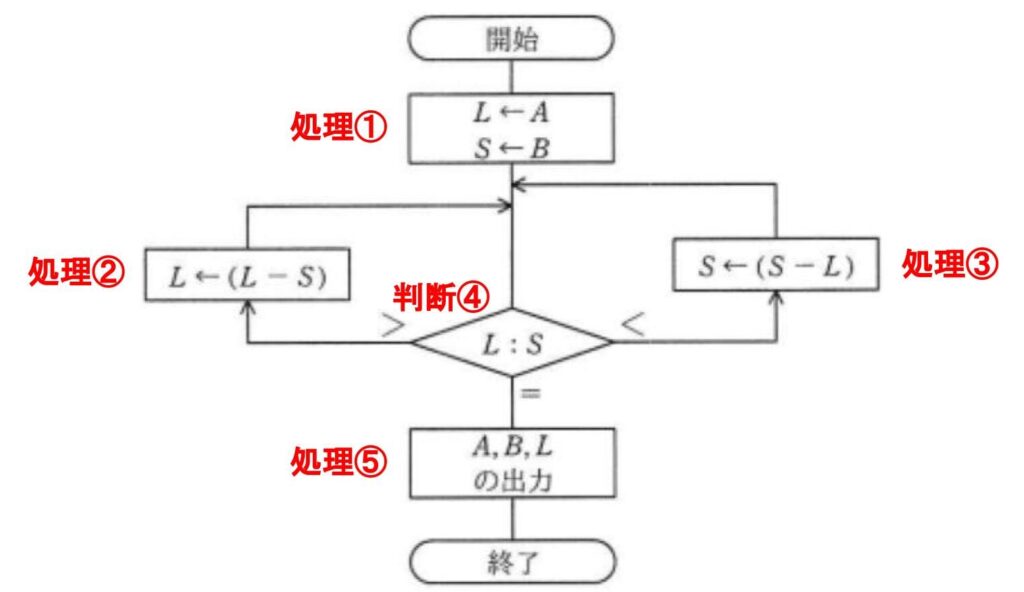
【アルゴリズム問題の鉄則③:1Stepずつ丁寧に見る】
処理①:L ← A、S ← B
・L=876
・S=204
判断④:LとSの比較(1回目)
L=876、S=204なので「>」
処理②:L ← (L-S)
L=876、S=204なので、処理②の後、L=672、S=204になります。
ここから先は下の表のようになります。
| 判断④(2回目) | LとSの比較 | L=672、S=204なので「>」 |
| 処理② | L ← (L-S) | 処理後はL=468、S=204 |
| 判断④(3回目) | LとSの比較 | L=468、S=204なので「>」 |
| 処理② | L ← (L-S) | 処理後はL=264、S=204 |
| 判断④(4回目) | LとSの比較 | L=264、S=204なので「>」 |
| 処理② | L ← (L-S) | 処理後はL=60、S=204 |
| 判断④(5回目) | LとSの比較 | L=60、S=204なので「<」 |
| 処理③ | S ← (S-L) | 処理後はL=60、S=144 |
| 判断④(6回目) | LとSの比較 | L=60、S=144なので「<」 |
| 処理③ | S ← (S-L) | 処理後はL=60、S=84 |
| 判断④(7回目) | LとSの比較 | L=60、S=84なので「<」 |
| 処理③ | S ← (S-L) | 処理後はL=60、S=24 |
| 判断④(8回目) | LとSの比較 | L=60、S=24なので「>」 |
| 処理② | L ← (L-S) | 処理後はL=36、S=24 |
| 判断④(9回目) | LとSの比較 | L=36、S=24なので「>」 |
| 処理② | L ← (L-S) | 処理後はL=12、S=24 |
| 判断④(10回目) | LとSの比較 | L=12、S=24なので「<」 |
| 処理③ | S ← (S-L) | 処理後はL=12、S=12 |
| 判断④(11回目) | LとSの比較 | L=12、S=12なので「=」 |
| 処理⑤ | 出力 | A,B,Lを出力 |
比較(判断④)の数は11回なので、答えはエになります。
平成29年度春期問5
基本情報技術者
午前試験 平成29年度春期問5
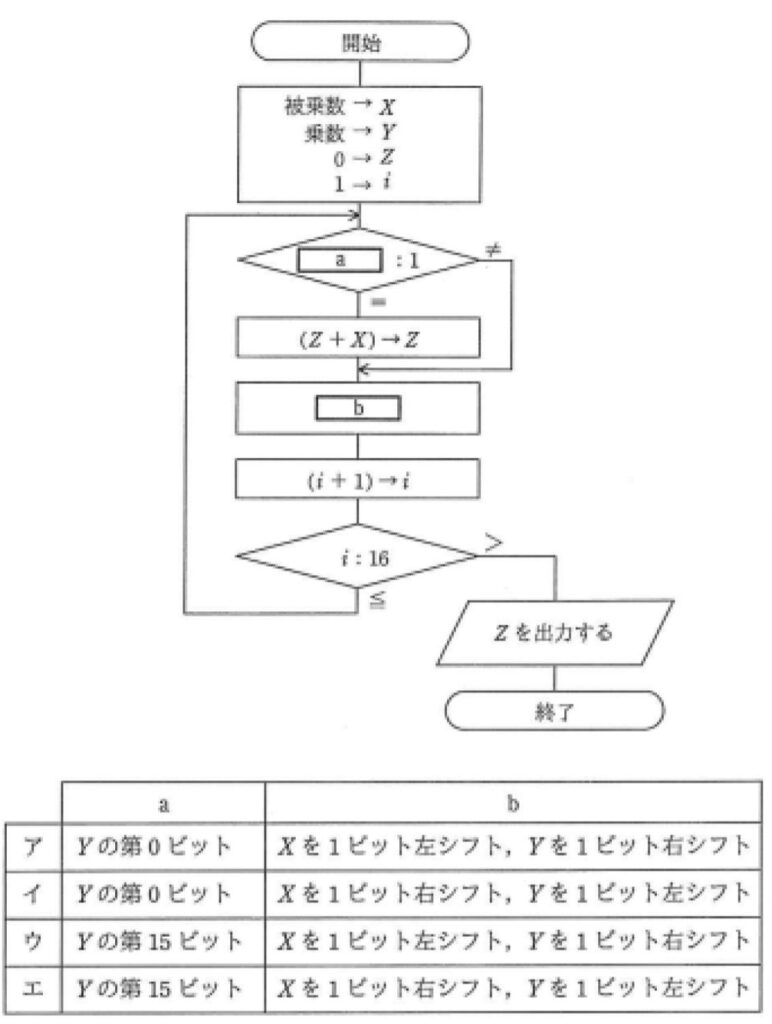
流れ図は,シフト演算と加算の繰り返しによって,2進整数の乗算を行う手順を表したものである。この流れ図中のa,bの組合せとして,適切なものはどれか。ここで,乗数と被乗数は符号なしの16ビットで表される。X,Y,Zは32ビットのレジスタであり,けた送りは論理シフトを用いる。最下位ビットを第0ビットと記す。
正解は”ア”
【アルゴリズム問題の鉄則①:具体的な数字を使う】
乗算についての問題なので、具体的な掛け算を使いましょう。
3×5=15
・乗数(掛ける数)=5 [2進数:0000 0000 0000 0101]
・被乗数(掛けられる数)=3 [2進数:0000 0000 0000 0011]
・答え=15 [2進数:0000 0000 0000 1111]
※乗数、被乗数は16ビット、XとYとZは32ビットと長いので0が続く所は0~0と表記します。
【アルゴリズム問題の鉄則②:処理と判断に着目する】
下の画像のように処理と判断に名前を付けてみます。
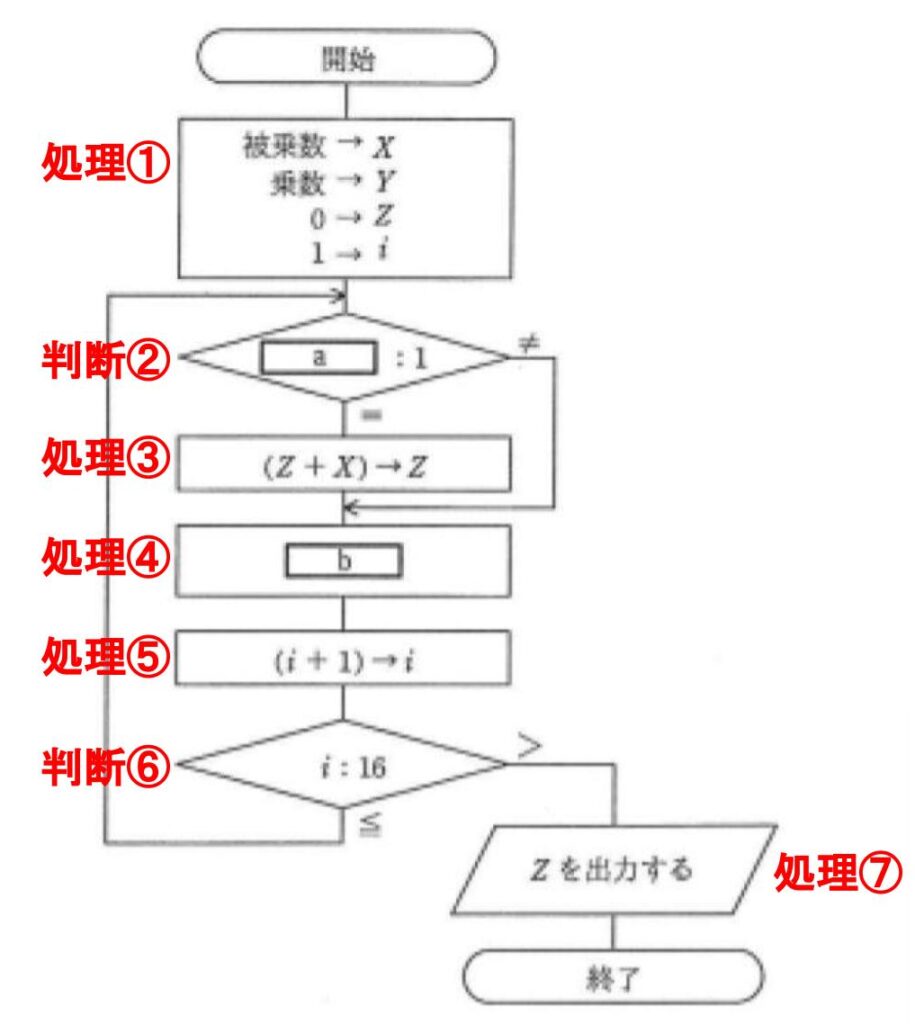
【アルゴリズム問題の鉄則③:1Stepずつ丁寧に見る】
処理①:各変数に数字を代入する
X=0000 0000 0000 0011, Y=0000 0000 0000 0101, Z=0, i=1
●i=1
判断②:Yの〇ビットと1を比較する
アとイ:Yの0ビットは1なので「=」(処理③へ)
ウとエ:Yの15ビットは0なので「≠」(処理④へ)
処理③:Z ← (Z+X)
アとイ:Z=0000 0000 0000 0011
処理④:XとYのシフト移動
ア:X=0000 0000 0000 0110, Y=0000 0000 0000 0010
イ:X=0000 0000 0000 0001, Y=0000 0000 0000 1010
ウ:X=0000 0000 0000 0110, Y=0000 0000 0000 0010
エ:X=0000 0000 0000 0001, Y=0000 0000 0000 1010
処理⑤:i ← (i+1)なので、i=2になる
判断⑥:i≠16なので、処理②へ
●i=2
判断②:Yの〇ビットと1を比較する
アとイ:Yの0ビットは0なので「≠」(処理④へ)
ウとエ:Yの15ビットは0なので「≠」(処理④へ)
この時点でイのYは、Y=0000 0000 0000 1010であり、
ここからいくら左に0ビットシフトしてもYの第0ビット=1になることはありません。つまり、イはこの先、処理③にいくことは無いので、最終的に出力されるZはこの時点でのZになります。
この時点での、イのZ=0000 0000 0000 0011
処理④:XとYのシフト移動
ア:X=0000 0000 0000 1100, Y=0000 0000 0000 0001
イ:X=0000 0000 0000 0000, Y=0000 0000 0001 0100
ウ:X=0000 0000 0000 1100, Y=0000 0000 0000 0001
エ:X=0000 0000 0000 0000, Y=0000 0000 0001 0100
この時点でエのXは、X=0000 0000 0000 0000であり、
ここからいくら右に0ビットシフトしてもX=0000 0000 0000 0000から
変わりません。つまり、エがこの先、処理③:Z ← (Z+X)に進んだとしても
X=0なので、Zの値は変わりません。なので、最終的に出力されるZはこの時点でのZになります。
この時点での、エのZ=0000 0000 0000 0000
処理⑤:i ← (i+1)なので、i=3になる
判断⑥:i≠16なので、処理②へ
●i=3
判断②:Yの〇ビットと1を比較する
ア:Yの0ビットは1なので「=」(処理③へ)
イ:Yの0ビットは0なので「≠」(処理④へ)
ウとエ:Yの15ビットは0なので「≠」(処理④へ)
処理③:Z ← (Z+X)
ア:Z=0000 0000 0000 1111(i=1の時のZとXの足し算結果)
処理④:XとYのシフト移動
ア:X=0000 0000 0001 1000, Y=0000 0000 0000 0000
イ:X=0000 0000 0000 0000, Y=0000 0000 0010 1000
ウ:X=0000 0000 0001 1000, Y=0000 0000 0000 0000
エ:X=0000 0000 0000 0000, Y=0000 0000 0010 1000
処理⑤:i ← (i+1)なので、i=4になる
判断⑥:i≠16なので、処理②へ
●i=4
判断②:Yの〇ビットと1を比較する
アとイ:Yの0ビットは0なので「≠」(処理④へ)
ウとエ:Yの15ビットは0なので「≠」(処理④へ)
※この時点でアとウのYは、Y=0000 0000 0000 0000であり、
ここからいくら右に0ビットシフトしてもY=0000 0000 0000 0000から
変わりません。つまり、アとウがこの先、処理③に行くことは無いので、
最終的に出力されるZはこの時点でのZになります。
この時点での、アのZ=0000 0000 0000 1111
この時点での、ウのZ=0000 0000 0000 0000
ここでア~エで出力されるZの値が全て判明しました。
ア:Z=0000 0000 0000 1111
イ:Z=0000 0000 0000 0011
ウ:Z=0000 0000 0000 0000
エ:Z=0000 0000 0000 0000
3×5=15になるはずで、15は2進数で0000 0000 0000 1111です。
これと一致するのはアなのでアが正解です。
基本情報に関する他の記事
| ハードウェア | ソフトウェア | システム構成 |
| ネットワーク | データベース | 開発手法 | 情報セキュリティ |
開発手法に関する記事
プログラムについての記事
【基本情報】午前試験のアルゴリズムの苦手意識を克服する!
【基本情報】関数?手続?再帰的?プログラムの性質を解説!
データ構造についての記事
【基本情報】スタックとキューってなに?どこで使われている?
【基本情報】2分探索木を完全に理解する!
【基本情報】ハッシュ法を完全に理解する!過去問と一緒に解説!
開発の流れについての記事
【基本情報】アジャイルを完全に理解する!過去問と一緒に解説!
【基本情報】UMLやDFDの全てをまとめて解説!
【基本情報】モジュール結合度について分かりやすく解説!
【基本情報】オブジェクト指向で出題されることをまとめた!
【基本情報】基本情報で出題されるテスト手法の全てを解説

