応用情報技術者では高頻度で直列接続と並列接続を比較する問題が出題されます。ここでマスターしましょう。

直列と並列
下の画像のように電池と電球を接続すると、電球は光ります。なぜなら、電池が電球に電気を供給しているからです。
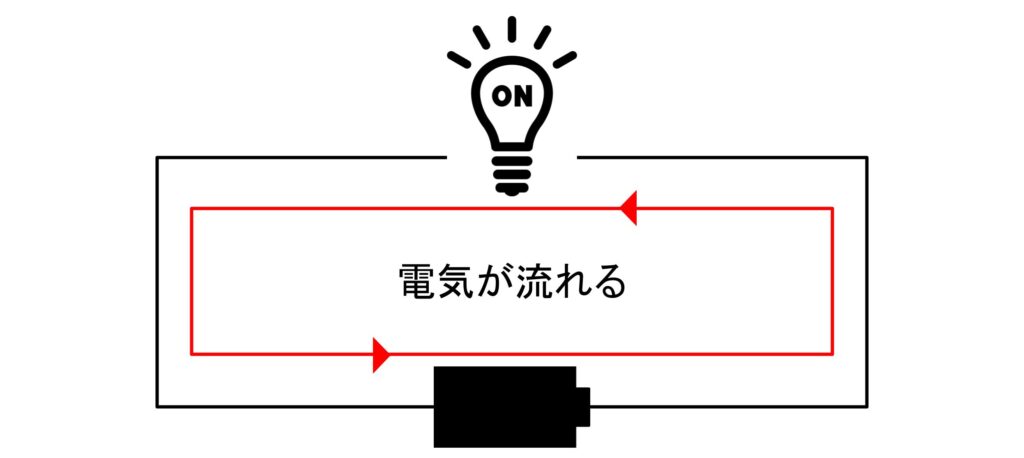
しかし、下の画像のように、電池切れを起こしたら、もちろん電球は光りません。なぜなら、電池が電球に電気を供給出来ないからです。
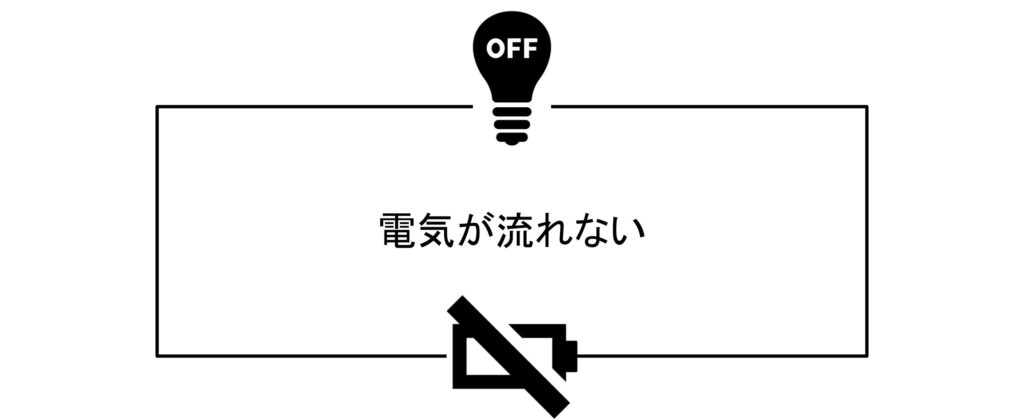
直列接続
では、電池を2つ直列に接続してみましょう。
下の画像のように使用可能な電池を2つ接続すれば、電球は光ります。
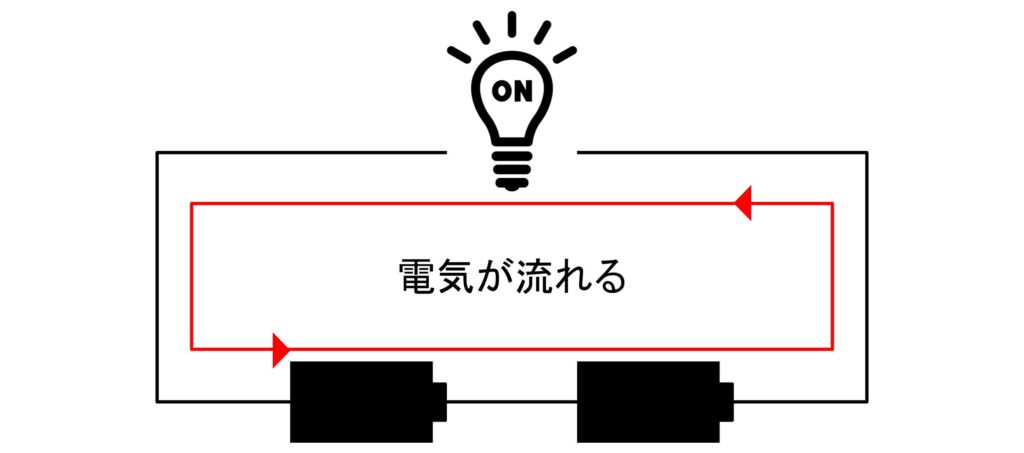
しかし、1つでも電池切れを起こしていた場合は電球は光りません。電池切れした電池は電気を通さず、電気は一周しないと働けないからです。
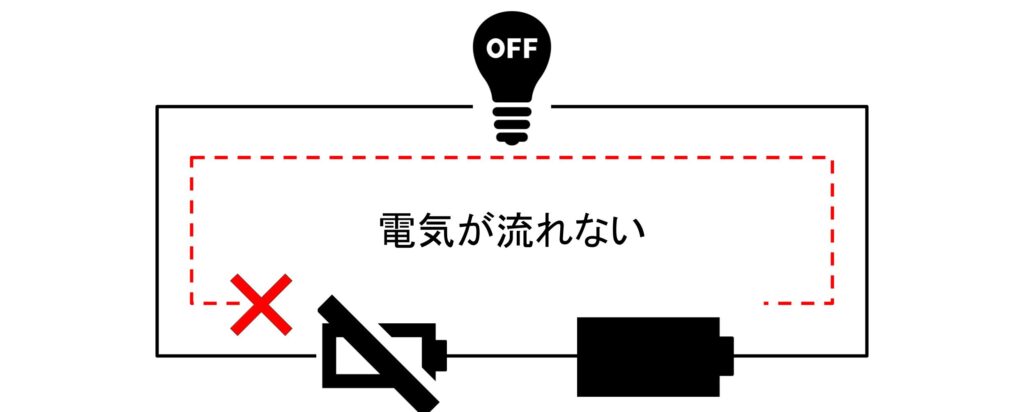
つまり、直列に電池を接続した場合、直列に接続された全ての電池が稼働していないと電球は光らないということです。
装置Aと装置Bが直列に接続されたシステムの稼働率の公式は下記のとおりです。
直列接続の稼働率の公式
システム全体の稼働率 = 装置Aの稼働率 × 装置Bの稼働率
具体例を見ていきます。
下の画像のように装置Aと装置Bを直列に接続したシステムの稼働率を考えます。
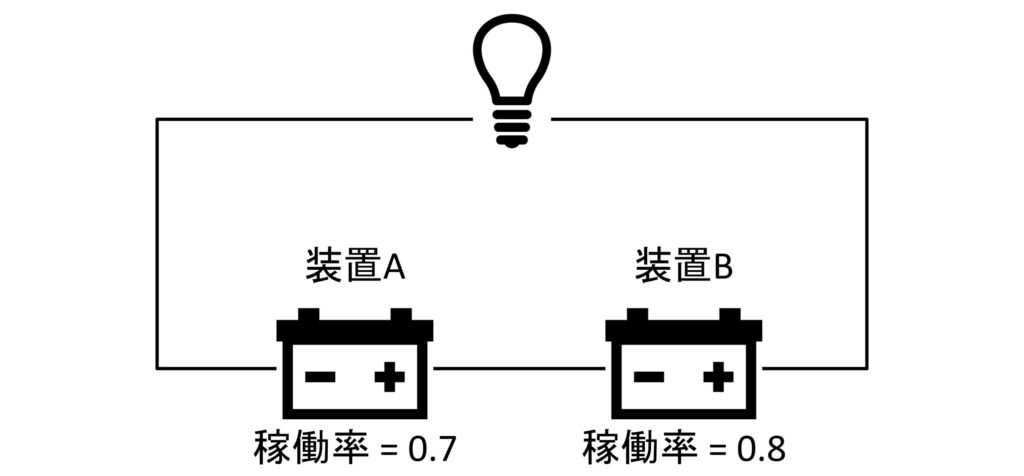
直列で接続された装置が全て稼働しないと、システムは動作しません。
よって、システム全体の稼働率は下の式で計算できます。
システム全体の稼働率 = 装置Aの稼働率 × 装置Bの稼働率
システム全体の稼働率 = 0.7 × 0.8 =0.56
並列接続
では、電池を2つ並列に接続してみましょう。
下の画像のように使用可能な電池を2つ接続すれば、電球は光ります。
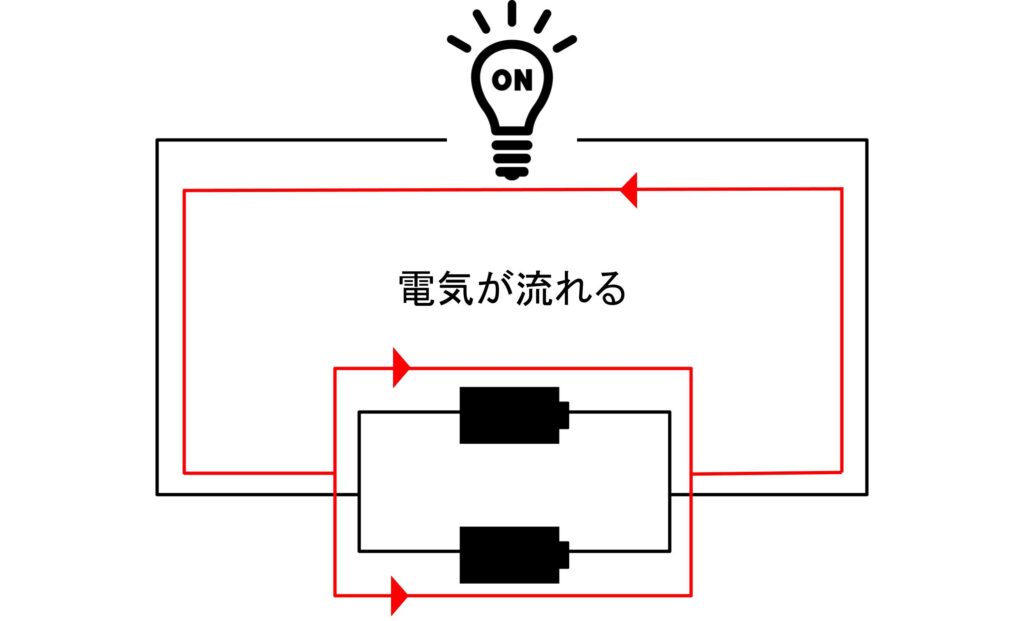
では、1つの電池が電池切れを起こしていたらどうでしょうか?この場合も、電球は光ります。下の電池の回路は電気が流れなくなりますが、上の電池の回路は電気が流れるので、電気が回路を一周出来ます。
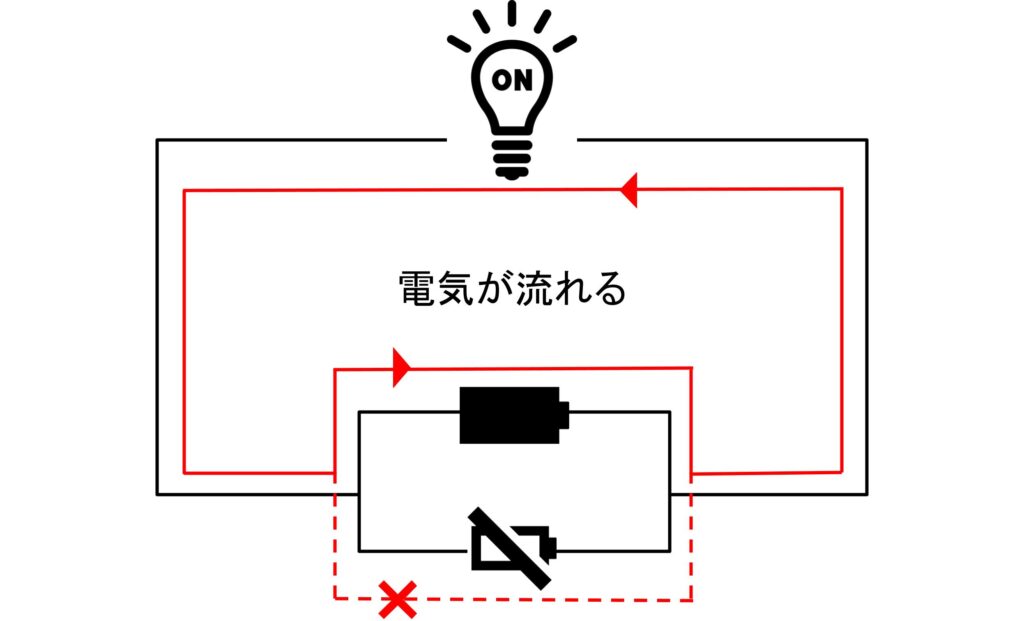
つまり、並列に電池を接続した場合、並列に接続された全ての電池が切れない限り電球は光り続けるということです。
装置Aと装置Bが並列に接続されたシステムの稼働率の公式は下記のとおりです。
並列接続の稼働率の公式
システム全体の稼働率 = 1 – (1 – 装置Aの稼働率) × (1 – 装置Bの稼働率)
具体例を見ていきます。
下の画像のように装置Aと装置Bを並列に接続したシステムの稼働率を考えます。
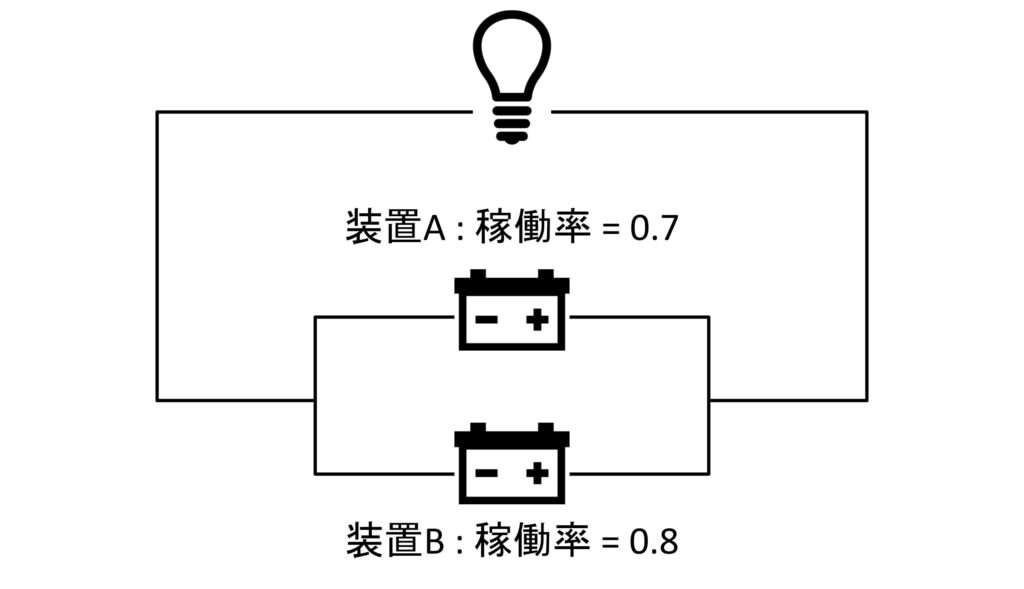
並列で接続された装置が全て故障しない限り、システムは稼働し続けます。
装置Aと装置Bが故障している確率は、それぞれ以下式で求めることが出来ます。
装置Aの故障率 = 1 – 装置Aの稼働率 = 1-0.7 = 0.3
装置Bの故障率 = 1 – 装置Bの稼働率 = 1-0.8 = 0.2
装置Aと装置Bの両方が故障したとき、システムは動かなくなります。
なので、システムの故障率は以下式で求めることが出来ます。
システムの故障率 = 装置Aの故障率 × 装置Aの故障率
システムの故障率 = 0.3 × 0.2 = 0.06
システムの故障率を求めることが出来たので、システムの稼働率は以下の式で求めることが出来ます。
システムの稼働率 = 1 – システムの故障率
システムの稼働率 = 1 – 0.06 = 0.94
この計算結果は並列接続した時の公式に当てはめた値と同じになります。
システム全体の稼働率 = 1 – (1 – 装置Aの稼働率) × (1 – 装置Bの稼働率)
システム全体の稼働率 = 1 – (1-0.7) × (1-0.8) = 0.94
直列と並列の両方を含むシステム
応用情報技術者試験では、直列と並列の両方を含むシステムの稼働率を問う問題があります。このようなシステムの稼働率はどのように計算するのでしょうか?
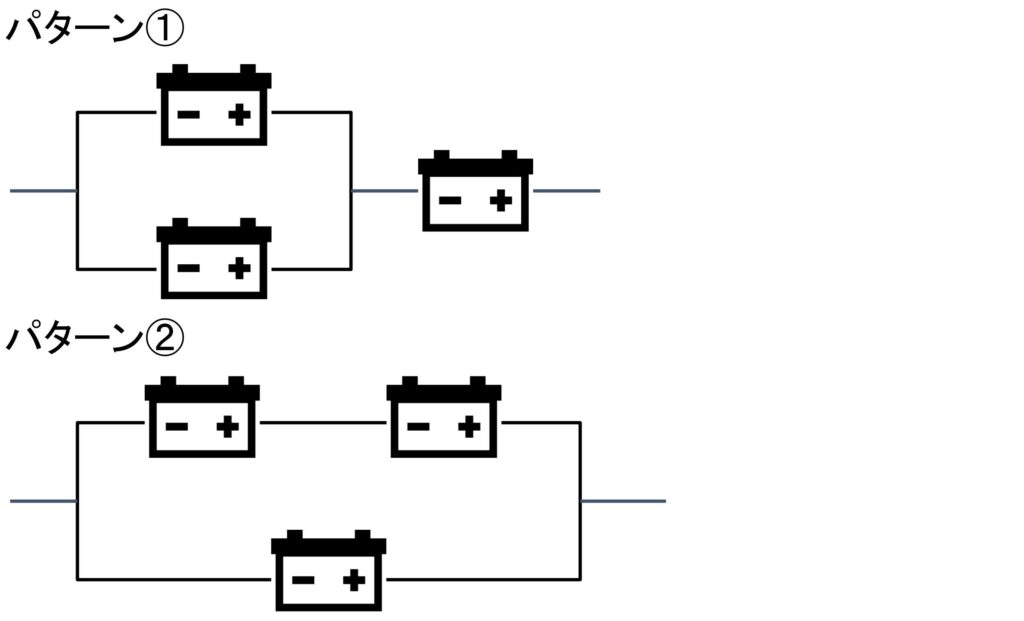
直列と並列を含むシステムの稼働率の計算方法
直列と並列を含むシステムの稼働率は下記の方法で計算できます。
- 直列接続している2つの装置を合体する。
- 並列接続している2つの装置を合体する。
- 全ての装置が合体するまで①と②を繰り返す。
例を見ていきましょう。
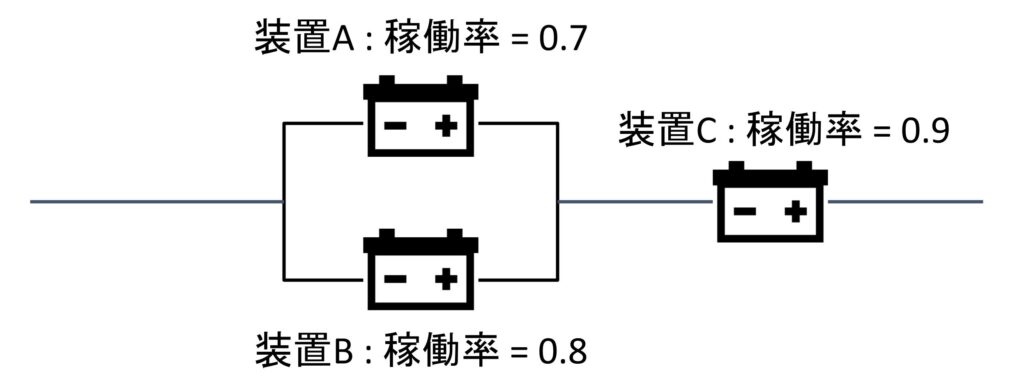
①直列接続している2つの装置を合体する。
直列接続している装置は無いので飛ばします。
②並列接続している2つの装置を合体する。
装置Aと装置Bが並列接続しているので合体して装置ABにしましょう。
装置ABの稼働率 = 1 – (1 – 0.7) × (1 – 0.8) = 0.94となります。
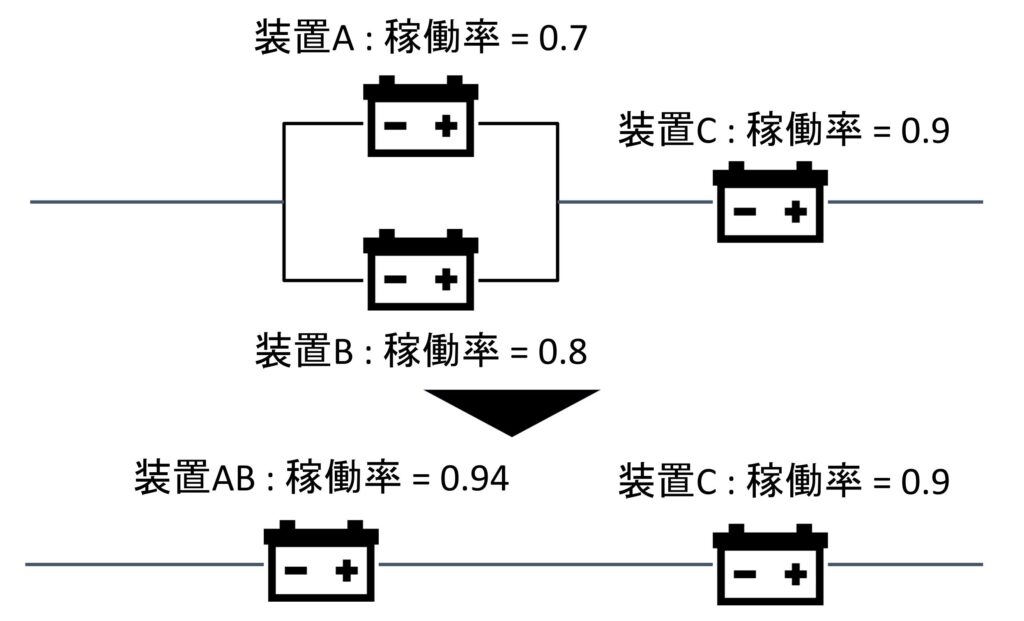
①直列接続している2つの装置を合体する。
装置ABと装置Cが直列接続しているので合体して装置ABCにしましょう。
装置ABCの稼働率 = 0.94×0.9 = 0.846となります。
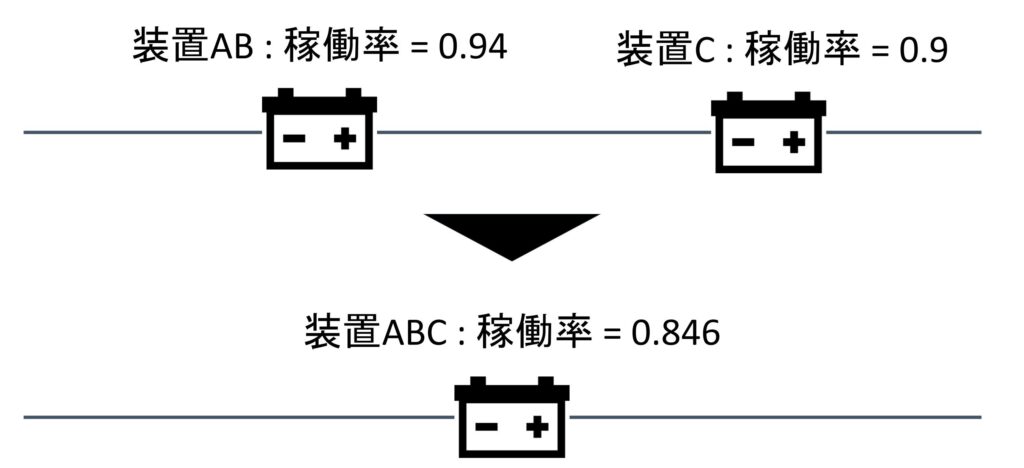
全ての装置が合体出来ました。このシステムの稼働率は0.846だと分かります。
応用情報技術者試験での出題
応用情報技術者試験を突破するのに必要な知識はこれだけです。

出題例
応用情報技術者 午前試験
令和5年度春期問16、平成30年度秋期問14
3台の装置X~Zを接続したシステムA,Bの稼働率に関する記述のうち、適切なものはどれか。ここで、3台の装置の稼働率は、いずれも0より大きく1より小さいものとし、並列に接続されている部分は、どちらか一方が稼働していればよいものとする。

ア 各装置の稼働率の値によって、AとBの稼働率のどちらが高いかは変化する。
イ 常にAとBの稼働率は等しい。
ウ 常にAの稼働率はBより高い。
エ 常にBの稼働率はAより高い。
正解は”エ”。
システムAとシステムBの稼働率を求めてみましょう。
装置X、Y、Zの稼働率をそれぞれX、Y、Zとします。
【システムA】
システムAは直列と並列が混ざっているシステムです。
なので、下の計算方法を使います。
- 直列接続している2つの装置を合体する。
- 並列接続している2つの装置を合体する。
- 全ての装置が合体するまで①と②を繰り返す。
①直列接続している2つの装置を合体する。
直列接続している装置は無いので飛ばします。
②並列接続している2つの装置を合体する。
装置Xと装置Yが並列接続しているので合体して装置XYにします。
装置XYの稼働率は並列接続の稼働率の公式を使って求めます。
装置XYの稼働率=1-(1-装置Xの稼働率)×(1-装置Yの稼働率)
=1-(1-X)×(1-Y) = 1-(1-X-Y+XY) = X-XY+Y

①直列接続している2つの装置を合体する。
装置XYと装置Zが直列接続しているので合体して装置XYZにします。
装置XYZの稼働率は直列接続の稼働率の公式を使って求めます。
装置XYZの稼働率=装置XYの稼働率×装置Zの稼働率
装置XYZの稼働率=(X-XY+Y)×Z = XZ-XYZ+YZ
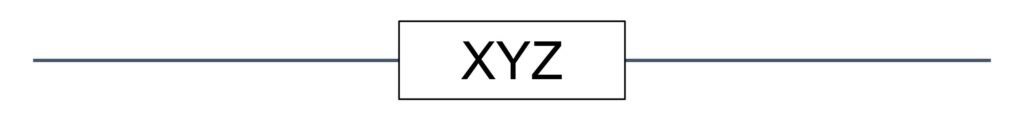
③全ての装置が合体するまで①と②を繰り返す。
全ての装置を合体出来ました。システムAの稼働率はXZ-XYZ+YZです。
【システムB】
システムBも直列と並列が混ざっているシステムです。
①直列接続している2つの装置を合体する。
装置Xと装置Zが直列接続しているので合体して装置XZにします。
装置XZの稼働率は直列接続の稼働率の公式を使って求めます。
装置XZの稼働率=装置Xの稼働率×装置Zの稼働率=XZ
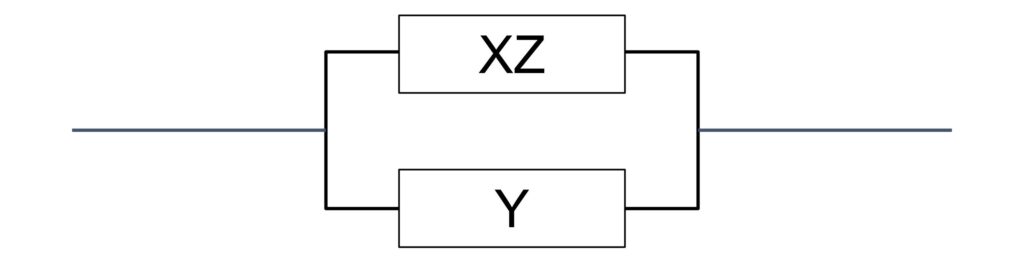
②並列接続している2つの装置を合体する。
装置XZと装置Yが並列接続しているので合体して装置XYZにします。
装置XYZの稼働率は並列接続の稼働率の公式を使って求めます。
装置XYZの稼働率=1-(1-装置XZの稼働率)×(1-装置Yの稼働率)
Z =1-(1-XZ)×(1-Y) = 1-(1-XZ-Y+XYZ) = XZ-XYZ+Y
③全ての装置が合体するまで①と②を繰り返す。
全ての装置を合体出来ました。システムBの稼働率はXZ-XYZ+Yです。
システムAとシステムBの稼働率を求めることが出来ました。
システムAの稼働率 = XZ-XYZ+YZ
システムBの稼働率 = XZ-XYZ+Y
「XZ-XYZ」は同じなので、Y×ZとYのどちらが大きいかになりますが、
問題文に「稼働率は0より大きく1より小さい」とあるので、Yの方が大きいです。
よって、システムBの稼働率の方が常に高いエが正解になります。
応用情報技術者 午前試験
令和3年度春期問14
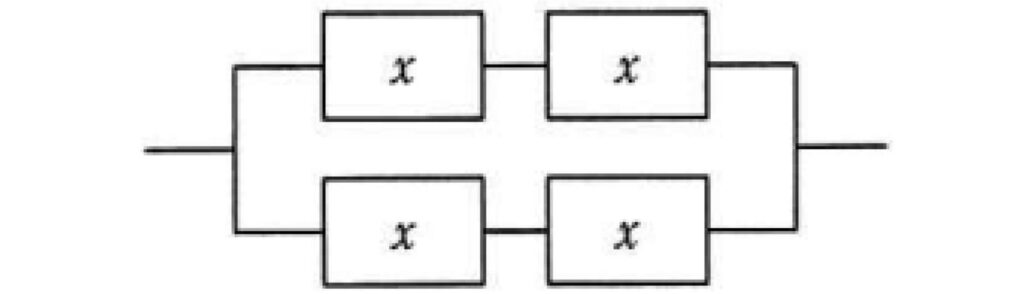
稼働率がxである装置を四つ組み合わせて,図のようなシステムを作ったときの稼働率をƒ(x)とする。区間 0≦x≦1 におけるy=ƒ(x)の傾向を表すグラフはどれか。ここで,破線はy=xのグラフである。
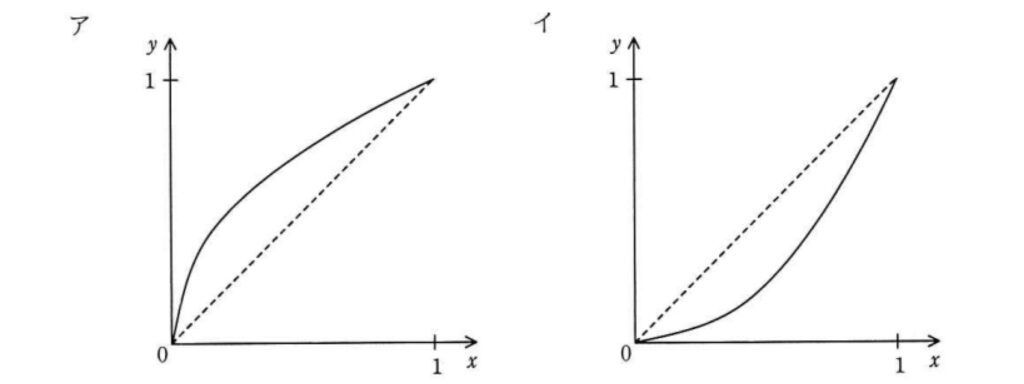
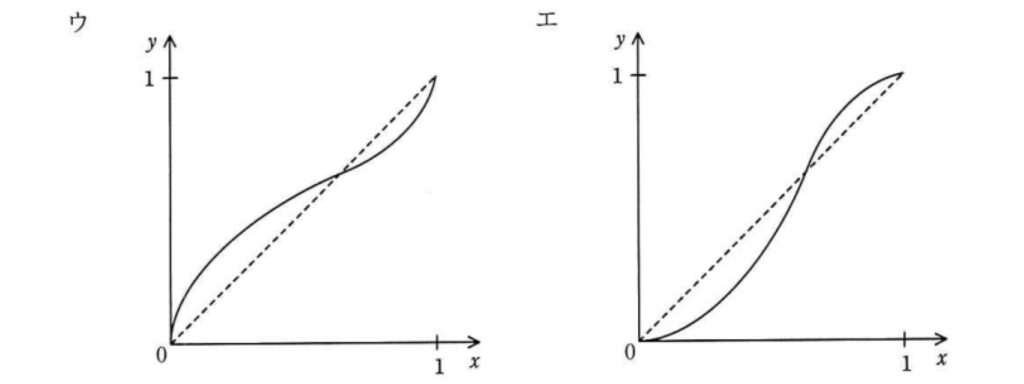
正解は”エ”。
問題のシステムの稼働率を求めてみましょう。
分かりやすくするためにそれぞれの装置に名前を付けます。
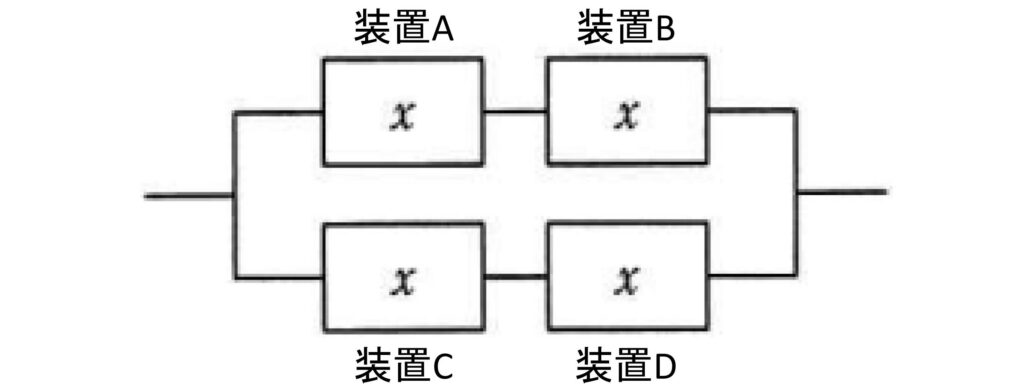
問題のシステムは直列と並列が混ざっているシステムです。
なので、下の計算方法を使います。
- 直列接続している2つの装置を合体する。
- 並列接続している2つの装置を合体する。
- 全ての装置が合体するまで①と②を繰り返す。
①直列接続している2つの装置を合体する。
装置Aと装置B、装置Cと装置Dはそれぞれ直列接続しているので、合体して装置ABと装置CDにします。装置ABと装置CDの稼働率は直列接続の公式を使って計算します。
装置ABと装置CDの稼働率 = X×X = X²
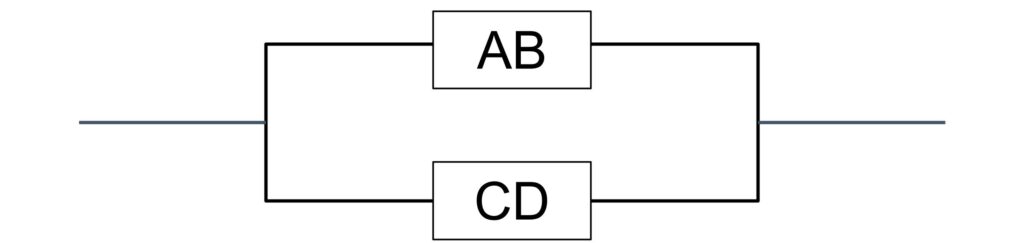
②並列接続している2つの装置を合体する。
装置ABと装置CDは並列接続しているので、合体して装置ABCDにします。
装置ABCDの稼働率は並列接続の公式を使って計算します。
装置ABCDの稼働率 = 1-(1-X²)×(1-X²)
装置ABCDの稼働率 = 1-(1-2X²+X⁴) = 2X²-X⁴ = X²(2-X²)
③全ての装置が合体するまで①と②を繰り返す。
全ての装置を合体出来ました。システムの稼働率はX²(2-X²)です。
システムの稼働率を求めることが出来たので、あとはX²(2-X²)とXの大小関係を調べます。
①X=0.1のとき
X²(2-X²) = 0.01 × (2-0.01) = 0.01 × 1.99 = 0.0199
よって、X=0.1のとき、X>X²(2-X²)となります。
②X=0.9のとき
X²(2-X²) = 0.81 × (2-0.81) = 0.81 × 1.19 = 0.9639
よって、X=0.9のとき、X²(2-X²)>Xとなります。
Xが小さいときは、Xの方が稼働率より大きくて、
Xが大きいときは、稼働率の方がXより大きいので、
答えはエになります。

